|
|
|
|
|
§ 10. Модели и моделирование
Списки, графы, деревья и таблицыМежду данными, используемыми в той или иной информационной модели, всегда существуют некоторые связи, определяющие ту или иную структуру данных.
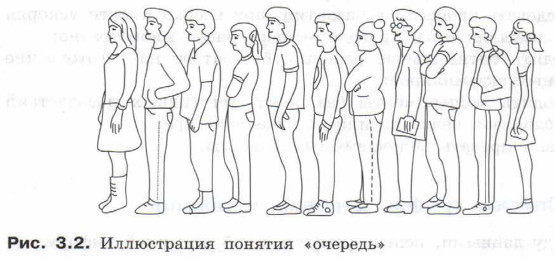
Различают линейные и нелинейные структуры данных. В курсе информатики основной школы вы познакомились с линейным односвязным списком — последовательностью линейно связанных элементов, для которых разрешены операции добавления элемента в произвольное место списка и удаление любого элемента. Связь элементов списка осуществляется за счёт того, что каждый элемент списка содержит кроме данных адрес элемента, следующего за ним в списке. В линейном списке для каждого элемента, кроме первого, есть предыдущий элемент; для каждого элемента, кроме последнего, есть следующий элемент. Частным случаем линейного односвязного списка является стек — последовательность, в которой включение и исключение элементов осуществляются с одной и той же стороны этой последовательности . Ещё одним частным случаем линейного односвязного списка является очередь — последовательность, у которой включение элементов производится с одной стороны последовательности, а исключение — с другой. Сторона, где происходит включение элементов, называется хвостом; сторона, где происходит исключение, — головой. Понятие очереди как структуры данных очень близко к бытовому понятию «очередь» (рис. 3.2).
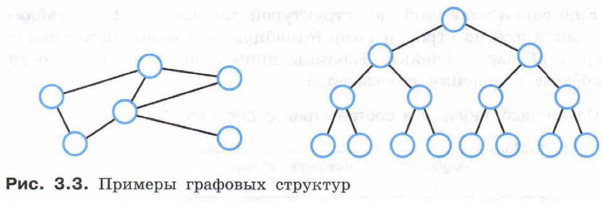
Почему стек является структурой типа LIFO (от англ. Last In, Firts Out — последним пришёл, первым ушёл)? Почему очередь является структурой типа FIFO (от англ. First In, First Out — первым пришёл, первым ушёл)? Примеры нелинейных структур данных вам также хорошо известны — это графы и деревья (рис. 3.3).
Граф — это множество элементов (вершин графа) вместе с набором отношений между ними. Граф является многосвязной структурой, обладающей следующими свойствами: 1) на каждый элемент может быть произвольное количество ссылок; 2) каждый элемент может иметь связь с любым количеством других элементов; 3) каждая связка может иметь направление и вес. Ненаправленная (без стрелки) линия, соединяющая вершины графа, называется ребром. Линия направленная (со стрелкой) называется дугой. При этом вершина, из которой дуга исходит, называется начальной, а вершина, куда дуга входит, — конечной. Граф называется неориентированным, если его вершины соединены рёбрами. Вершины ориентированного графа соединены дугами. Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер. Графы являются основным средством для описания структур сложных объектов. С их помощью можно описать вычислительную сеть, транспортную систему, схему авиалиний и другие объекты. Одной из разновидностей графа является дерево. Дерево — это совокупность элементов (вершин), в которой выделен один элемент (корень), а остальные элементы разбиты на непересекающиеся множества (поддеревья). Каждое поддерево является деревом, а его корень является потомком корня дерева, т. е. все элементы связаны между собой отношением «предок — потомок». В результате образуется иерархическая структура вершин. Частным случаем дерева является бинарное дерево, в котором каждая вершина может иметь не более двух потомков. Деревья используются для представления родственных связей (генеалогическое дерево), для определения выигрышной стратегии в играх и т. д. Ещё одной знакомой вам структурой данных являются таблицы, состоящие из строк и граф (столбцов, колонок), пересечение которых образуют ячейки. Таблицы применяют для наглядности и удобства сравнения показателей.
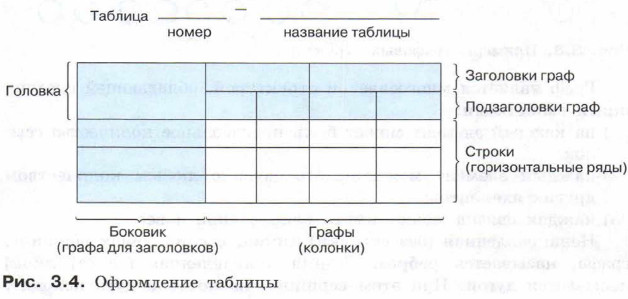
Название таблицы, при его наличии, должно отражать её содержание, быть точным, кратким. Название следует помещать над таблицей. Заголовки граф и строк таблицы следует писать с прописной буквы, а подзаголовки граф — со строчной буквы, если они составляют одно предложение с заголовком, или с прописной буквы, если они имеют самостоятельное значение. В конце заголовков и подзаголовков таблицы точки не ставят. Заголовки и подзаголовки граф указывают в единственном числе. Если все показатели, приведённые в графах таблицы, выражены в одной и той же единице физической величины, то её обозначение необходимо помещать над таблицей справа. Если в графе таблицы помещены значения одной и той же физической величины, то обозначение единицы физической величины указывают в заголовке (подзаголовке) этой графы. Эти и другие требования к оформлению таблиц содержатся в ГОСТ 2.105-95 «ЕСКД. Общие требования к оформлению текстовых документов». В курсе информатики основной школы вы познакомились с таблицами типа:
Таблицы, в которых отражено наличие или отсутствие связей между отдельными элементами некоторой системы, называются двоичными матрицами.
Табличный способ представления данных является универсальным — любую структуру данных, в том числе и представленную в форме графа, можно свести к табличной форме. Это тем более важно в связи с тем, что для компьютерной обработки табличное представление данных является предпочтительным.
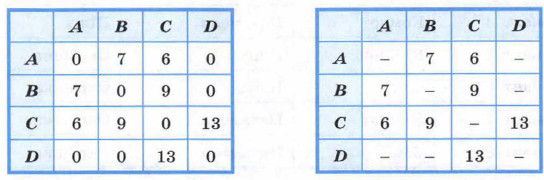
Строки и столбцы таблицы будут соответствовать вершинам графа. Если две вершины являются смежными (соединены ребром), то в ячейку на пересечении соответствующих столбца и строки будем записывать вес этого ребра. В противном случае (вершины не являются смежными) в ячейку будем записывать 0. Получится таблица типа «объект — объект». Такую таблицу называют матрицей смежности. Часто в матрицах смежности вместо нуля ставят знак минус, что обеспечивает большую наглядность.
Матрица смежности неориентированного графа симметрична относительно главной диагонали, идущей от левого верхнего угла к правому нижнему углу. У матрицы смежности неориентированного графа такая симметрия отсутствует.
|
Вспомните, как мы определяли структуру данных при рассмотрении алгоритмов и программ. О каких информационных моделях тогда шла речь? С какими структурами данных вы сталкивались в программировании?
Оформляют таблицы в соответствии с рисунком 3.4.
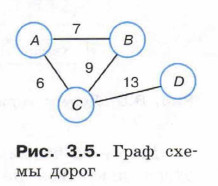
Пример 1. Построим таблицу, соответствующую неориентированному графу (рис. 3.5), отражающему схему дорог между некоторыми населёнными пунктами.
|
|