|
|
|
|
|
§ 10. Модели и моделирование 10.3. Списки, графы, деревья и таблицы
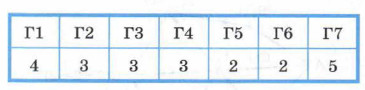
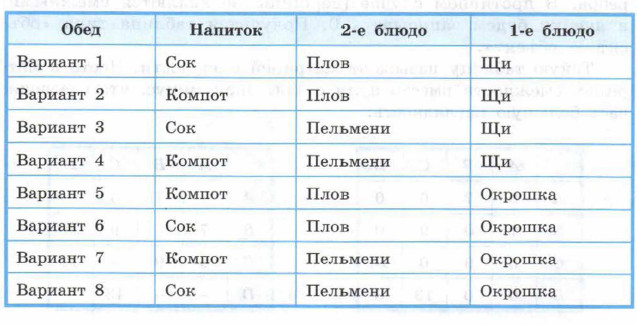
Для того чтобы представить эту же информацию в таблице, будем двигаться по дереву от листьев к корню, описывая все возможные варианты обеда.
Получилась таблица типа «объект-свойства»: объектами в ней являются варианты обеда, а свойствами — составляющие его блюда. При этом число граф в полученной таблице соответствует числу уровней в дереве. При решении класса задач, связанного с нахождением кратчайшего пути в ориентированном графе, можно: 1) от исходного графа перейти к матрице смежности; 2) по матрице смежности построить дерево решений; 3) по дереву решений выбрать подходящий вариант.
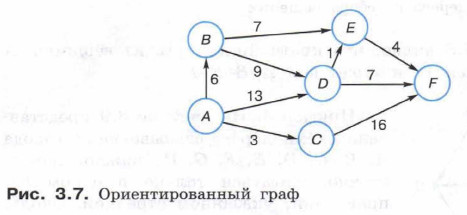
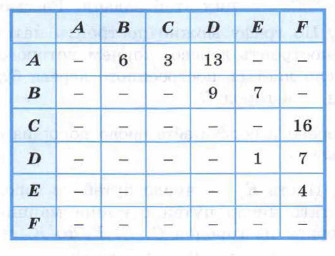
Составим матрицу смежности, соответствующую данному ориентированному графу:
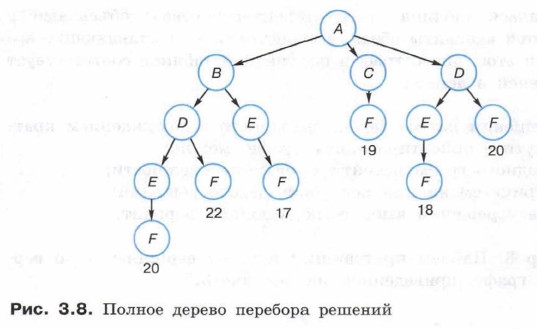
По матрице смежности построим полное дерево перебора решений — рисунок 3.8.
На рисунке 3.8 видно, что кратчайший путь из вершины А в вершину F равен 17 и имеет вид A-B-E-F.
Существует несколько способов решения этой задачи. Рассмотрим их. Вариант 1. По графу можно построить матрицу смежности, а на её основе построить дерево, корнем которого будет служить вершина А. Число листьев построенного дерева будет равно числу дорог из города А в город G.
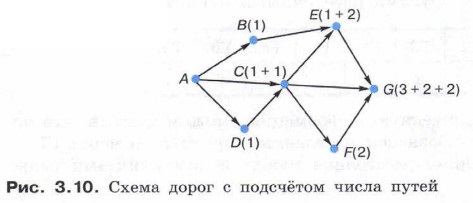
Вариант 2. Пусть КХ — число путей из города А в город X. Начнем считать число путей с конца маршрута. Так как в город G есть дороги из городов С, Е, F, то KG = КС + КЕ + KF. В свою очередь КС = 1 + KD = 1 + 1 = 2, КЕ = КВ + КС = 1 + 2 = 3, KF = КС = 2. Таким образом, KG = 2 + 3 + 2 = 7. Вариант 3. Можно считать число путей с начала маршрута. При этом процесс подсчёта удобно изображать на самом графе — рисунок 3.10.
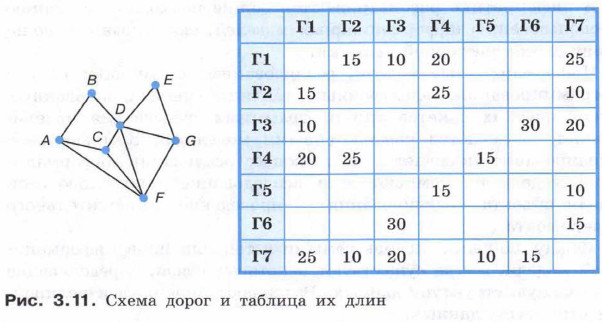
Рассмотрим имеющийся граф и выясним степень каждой вершины — число рёбер, соединяющих некоторую вершину с другими вершинами. Получим:
На основании имеющейся таблицы мы также можем сделать выводы о том, сколькими дорогами соединён тот или иной населённый пункт с другими населёнными пунктами:
Сопоставив полученную информацию, можем сказать, что через Г1 в таблице обозначен населённый пункт F, а через Г7 — D. Согласно таблице, расстояние между этими пунктами равно 25 км.
|
|
|



 Пример 2. Обед в школьной столовой состоит из двух блюд и напитка. На первое можно выбрать щи или окрошку, на второе — плов или пельмени, на третье — сок или компот. Все возможные варианты представлены с помощью дерева на рисунке 3.6.
Пример 2. Обед в школьной столовой состоит из двух блюд и напитка. На первое можно выбрать щи или окрошку, на второе — плов или пельмени, на третье — сок или компот. Все возможные варианты представлены с помощью дерева на рисунке 3.6.
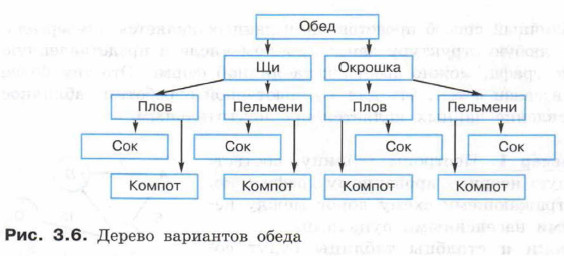
 Пример 4. На рисунке 3.9 представлена схема дорог, связывающих города А, В, С, D, Е, F, G. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько разных путей существует из города А в город G?
Пример 4. На рисунке 3.9 представлена схема дорог, связывающих города А, В, С, D, Е, F, G. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько разных путей существует из города А в город G?
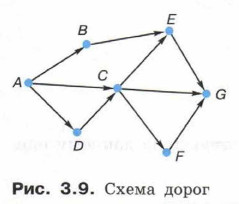
 Постройте дерево и подсчитайте число дорог из города А в город G самостоятельно.
Постройте дерево и подсчитайте число дорог из города А в город G самостоятельно.