Главная >> Информатика 11 класс. Босова

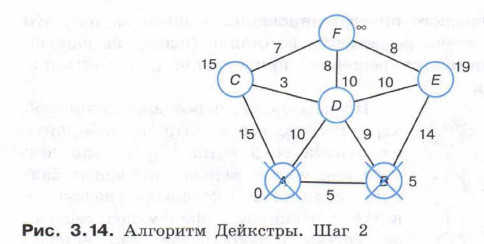
§ 11. Моделирование на графах

11.1. Алгоритмы нахождения кратчайших путей между вершинами графа

После изменения меток всех соседей вершины А она помечается как просмотренная. Теперь минимальная метка из непросмотренных вершин у вершины В. Её соседи — вершины D и Е. Так как 5 + 9 > 10, метка вершины D не изменяется. Вершина Е получает метку 19 (рис. 3.14).

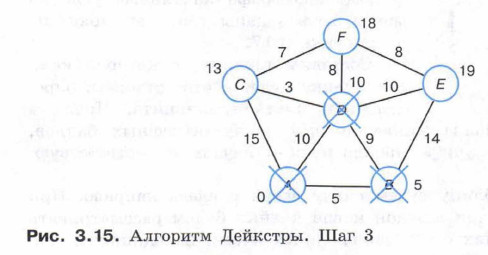
Теперь минимальная метка из непросмотренных вершин у вершины I). Её соседи — вершины С, Е и F. Так как 10 + 3 < 15, метка вершины С изменяется. Вершина F получает метку 18. Метка вершины Е не изменяется (рис. 3.15).

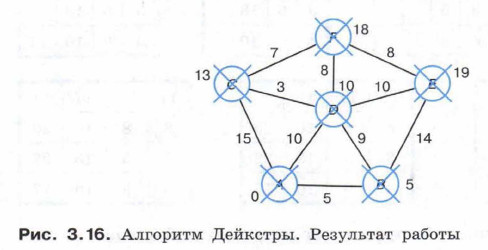
Далее в качестве вершин с минимальными метками будут поочерёдно рассматриваться вершины С, F и Е. К изменению меток соседних с ними вершин это не приведёт (рис. 3.16).

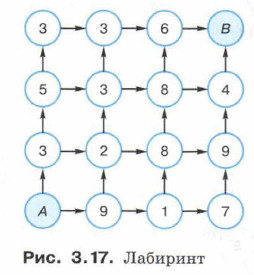
Полученные в результате работы алгоритма метки вершин графа — это и есть кратчайшие расстояния от вершины А до каждой из этих вершин.

Метод динамического программирования основан на том, что процесс решения задачи разбивается на стадии (шаги), на каждой из которых принимаются решения, приводящие к достижению поставленной цели.

Предположим, персонажу некоторой игры необходимо пройти по лабиринту из пункта А в пункт В, набрав при этом как можно меньше штрафных баллов, количество которых указано в клетках лабиринта, причём перемещаться можно только вверх или вправо. С помощью графа начальные условия могут быть заданы так, как показано на рисунке 3.17.

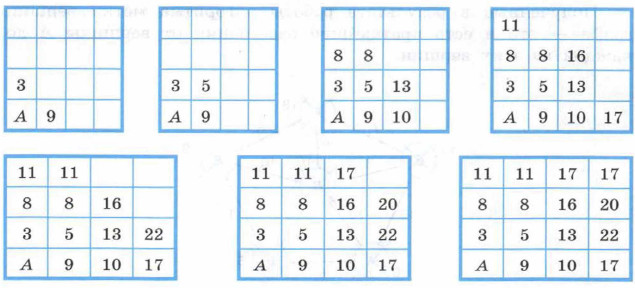
Составим таблицу, в которой каждая ячейка будет соответствовать определённой клетке лабиринта. Числа в ячейках будут равны минимальному числу штрафных баллов, которое можно получить, пройдя путь от начала до соответствующей клетки.

Заполнять таблицу будем снизу вверх и слева направо. При этом для заполнения каждой новой ячейки будем рассматривать числа двух соседних с ней заполненных ячеек, находящихся слева от неё и под ней. Будем выбирать наименьшее из этих двух чисел, прибавлять к ним число текущей ячейки и результат записывать в неё.

Ответ равен числу в правом верхнем углу таблицы.

Давайте считать, что числа, обозначающие веса вершин рассмотренного графа, — это призовые баллы, которые можно получить, пройдя по соответствующим клеткам лабиринта. Самостоятельно подсчитайте, какое максимальное число призовых баллов можно набрать, пройдя этот лабиринт.

<<< К началу