Знакомство с теорией игр

Рассмотрим несколько примеров.

Пример 1.

Алёша Попович и Добрыня Никитич воюют с девятиглавым змеем. По очереди богатыри ходят к его пещере и срубают 1, 2 или 3 головы. Как начавшему бой Алёше обрести славу победителя змея (срубить последнюю голову), если и Добрыня готов приложить все усилия, чтобы стать победителем в этой битве?

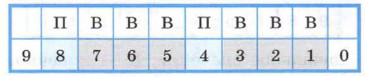
Изобразим на числовой линейке текущее число голов змея:

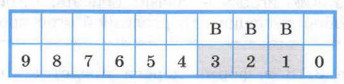
Здесь: 9 — начальное значение; 0 — конечное значение (победа).

Алёша обретёт славу победителя, если после его последнего удара у змея останется 0 голов. Для этого нужно, чтобы после очередного удара Добрыни у змея осталось 3, 2 или 1 голова. Иначе говоря, позиции 3, 2 и 1 являются для Алёши выигрышными (как, впрочем, для любого из богатырей, кому они достаются в качестве исходных при последнем ударе). Выигрышные и проигрышные позиции на числовой линейке будем помечать буквами «В» и «П» соответственно:

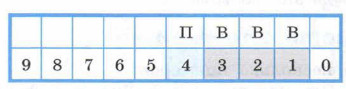
Если Добрыня выйдет на бой с черырёхголовым змеем (будет находиться в позиции 4), то любым своим ударом он создаст Алёше условия для выигрыша (переведёт Алёшу в выигрышную позицию). Следовательно, задача Алёши на предыдущем шаге состоит в том, чтобы перевести Добрыню в эту заведомо проигрышную для него позицию:

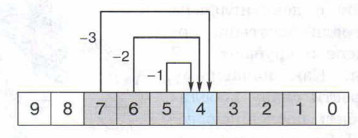
Четырёхголового соперника Алёша сможет обеспечить Добрыне, если сам будет находиться в одной из позиций 7, б или 5:

Любой удар Добрыни приведёт к благоприятному для Алёши результату только в том случае, если Добрыня выйдет на бой с восьмиголовым змеем:

Следовательно, первым своим ударом Алёша должен срубить змею одну голову.

Выигрышная стратегия — это правило, следуя которому игрок выигрывает независимо от того, как играет противник.
Игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Выигрышная стратегия может быть только у одного игрока.
Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации при различной игре противника.

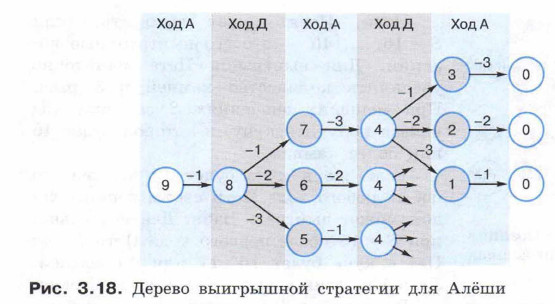
На рисунке 3.18 в форме дерева представлена выигрышная стратегия для Алёши. Поэтому для Алёши всегда указывается один ход («Ход А»), обеспечивающий требуемый результат. А вот для Добрыни, фактически выступающего в качестве соперника, рассматриваются все возможные варианты («Ход Д»).

Дерево выигрышной стратегии для Алёши

Пример 2. А эта задача из открытого банка заданий ЕГЭ по информатике (fipi.ru).

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя.

За один ход игрок может выполнить одно из следующих действий:

добавить в кучу один камень (+ 1);
добавить в кучу два камня (+ 2);
увеличить количество камней в куче в 3 раза (х 3).

Например, имея кучу из 5 камней, за один ход можно получить кучу из 6, 7 или 15 камней.

У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче превышает 45. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 46 или больше камней. Будем считать, что в начальный момент в куче S камней, 1 ≤ S ≤ 45.

Выясним, при каких значениях числа S Петя может выиграть первым ходом.

Если S = 45, то, добавив в кучу один камень (+ 1), два камня (+ 2) или утроив количество камней в ней (х 3), Петя становится победителем.

Если S = 44, то стать победителем можно, если добавить в кучу два камня (+ 2) или утроить количество камней в ней (х 3).

Если S = 43, то Петя становится победителем, утроив количество камней в куче (х 3). Также можно действовать для любого S ≥ 16 (16 х 3 = 48, 15 х 3 = 45).

Окончание >>>