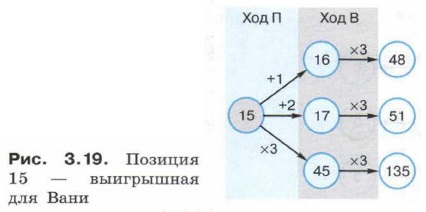
11.2. Знакомство с теорией игр

Итак, Петя может выиграть, если S = 16, ..., 45 — это его выигрышные позиции. Для выигрыша Пете достаточно увеличить количество камней в 3 раза. При меньших значениях S за один ход нельзя получить кучу, в которой будет 46 или более камней.

Если же в куче будет 15 камней, то после любого хода Пети своим первым ходом может выиграть Ваня. Действительно, при S = 15 после первого хода Пети («Ход П») в куче будет 16, 17 или 45 камней. Любой из этих случаев является выигрышным для делающего ход Вани («Ход В»), которому для победы достаточно увеличить количество камней в 3 раза (рис. 3.19).

Позиция 15 — выигрышная для Вани

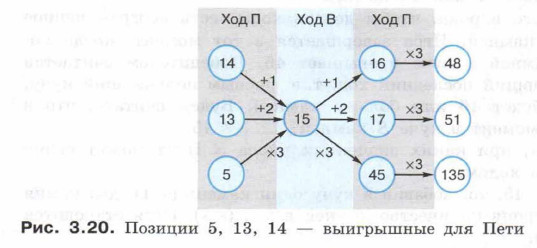
Теперь попробуем определить значения S, при которых у Пети будет выигрышная стратегия, причём Петя не сможет выиграть первым ходом, но сможет выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.

Мы выяснили, что S = 15 — проигрышная позиция для любого игрока. Если Петя своим первым ходом сможет перевести в неё Ваню, то что бы ни делал последний, сам он выиграть не сможет, но переведёт в выигрышную позицию своего соперника. 15 камней Петя может получить при S = 14 (+ 1), S = 13 (+ 2) или S = 5 (х 3). Других вариантов для S нет (рис. 3.20).

Позиции 5, 13, 14 — выигрышные для Пети

Представим всю информацию на числовой линейке:

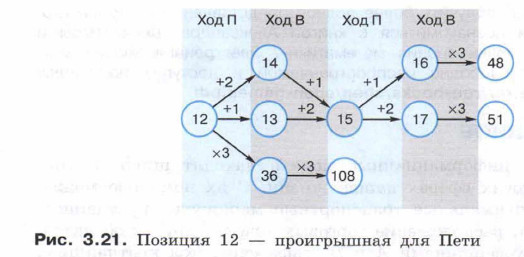
Найдём на ней такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Здесь речь идёт о проигрышной позиции для первого игрока. Следовательно, искать значение S надо среди позиций, не отмеченных как выигрышные.

Пусть S = 12. Каким бы ни был ход Пети, им он переведёт своего соперника в выигрышную позицию: 13(12 + 1), 14 (12 +2) или 36 (12 х 3). В последнем случае Ваня имеет возможность выиграть своим первым же ходом (36 х 3), а в первых двух случаях он должен перевести соперника в проигрышную позицию *S = 15, что обеспечит ему выигрыш вторым ходом. Следовательно, позиция S = 12 — проигрышная для Пети. На дереве решений наши рассуждения могут быть представлены так, как показано на рисунке 3.21.

Позиция 12 — проигрышная для Пети

Если вместо S = 12 взять S = 11, то приведёт ли любой ход Пети Ваню к выигрышу? Подойдёт ли для этой цели S = 10? Обоснуйте свой ответ.

Примеры, которые мы рассмотрели, имеют самое непосредственное отношение к теории игр — разделу современной математики, связанному с решением многих задач экономики, социологии, политологии, биологии, искусственного интеллекта и ряда других областей, где необходимо изучение поведения человека и животных в различных ситуациях.

Игра выступает в качестве математической модели некоторой ситуации и понимается как процесс, в котором участвуют две и более стороны, ведущие борьбу за реализацию своих интересов. При этом игра характеризуется такими признаками, как:

1) присутствие нескольких игроков;

2) неопределённость поведения игроков, связанная с имеющимися у каждого из них несколькими вариантами действий;

3) различие (несовпадение) интересов игроков;

4) взаимосвязанность поведения игроков (результат, получаемый каждым из них, зависит от поведения всех игроков);

5) наличие правил поведения, известных всем игрокам.

Игра может быть представлена в виде дерева, каждая вершина которого соответствует ситуации выбора игроком своей стратегии.

Примеры, которые мы рассмотрели, относятся к так называемым играм с полной информацией. В играх с полной информацией участники знают все ходы, сделанные до текущего момента, равно как и возможные стратегии противников, что позволяет им в некоторой степени предсказать последующее развитие игры.

Тем, кто хочет получить более полное представление о теории игр, рекомендуем познакомиться с книгой Александра Шеня «Игры и стратегии с точки зрения математики». Электронная версия книги является свободно распространяемой и доступна по адресу www.mccme.ru/free-books/shen/shen-games.pdf.

<<< К началу