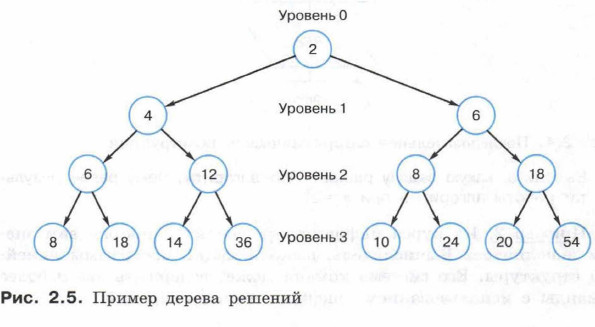
|
|
|
|
|
§ 6. Алгоритмические структуры
6.1. Последовательная алгоритмическая конструкцияДля удобства поиска числа разных вариантов значений, которые будут получены по этим программам, составим дерево решений (рис. 2.5). В его корневой вершине (0-й уровень) записывается начальное значение. Ветви дерева соответствуют командам: левые — первой, правые — второй. В каждой вершине дерева 1-го, 2-го и т. д. уровней записывается результат, полученный после применения команды к числу из вершины-предка. Путь к каждой из вершин соответствует последовательности команд (программе) для получения значения, находящегося в вершине. Таким образом в вершинах N-го уровня будут записанны результаты программ, состоящих из N команд.
В нашем примере все значения в вершинах третьего уровня различны. Иногда значения в вершинах одного уровня совпадают. Можно сказать, что в общем случае число различных значений на уровне не превышает числа его вершин. Номер уровня, на котором впервые появляется необходимое число, равен минимальному количеству команд для его получения. В нашем примере число 8 записано в вершинах 2-го и 3-го уровней, следовательно, минимальное количество команд для его получения равно двум. Для определения количества программ, с помощью которых требуемое число получается из заданного, можно подсчитать количество вершин дерева, в которых записано требуемое число.
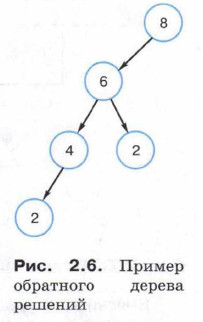
Если количество уровней вершин в дереве решений превышает четыре, то строить такое дерево неудобно. Так же как и в случае, когда система команд исполнителя состоит из трёх и более команд. Для некоторых задач удобнее строить обратное дерево решений: команды исполнителя меняются на «обратные», пути строятся от результата к начальному значению. На рисунке 2.6 показан пример построения обратного дерева решений (из числа 8 получаем число 2; команды: 1) вычти 2; 2) раздели на 3).
Этот приём удобно использовать, когда обратные команды неприменимы ко всем вершинам.
|
Подумайте, почему при заданных условиях существует только две программы для получения из числа 2 числа 8.
|
|