|
|
|
|
|
§ 2. Сложение и вычитание натуральных чисел 10. Уравнение (продолжение)
375. Решить уравнение (у + 64) - 38 = 48 можно двумя способами: 1) сначала найти неизвестное уменьшаемое у 4-64:
или
Подобным образом решите двумя способами уравнение: а) (х + 98) + 14 = 169; б) (35 + у) - 15 = 31. 376. Решите уравнение и выполните проверку: а) (х + 15) - 8 = 17; г) (у - 35) + 12 = 32;
377. Решите с помощью уравнения задачу: а) Витя задумал число. Если к этому числу прибавить 23 и к полученной сумме прибавить 18, то будет 52. Какое число задумал Витя?
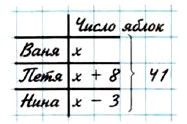
378. Запишите в виде равенства:
а) У Вани было х яблок, у Пети — на 8 яблок больше, а у Нины — на 3 яблока меньше, чем у Вани. Вместе у них было 41 яблоко. б) Один токарь выточил у деталей, другой — на 7 деталей больше, чем первый, а третий — на 8 деталей меньше, чем второй. Вместе они сделали 81 деталь. в) У Кости п открыток, у Игоря — на 8 открыток меньше, чем у Кости, а у Наташи — на 15 открыток больше, чем у Кости. У Наташи столько же открыток, сколько у Кости и Игоря вместе. г) В первый сосуд налили т л жидкости, во второй — на 7 л меньше, чем в первый, а в третий сосуд — на 10 л больше, чем во второй. В третьем сосуде оказалось столько жидкости, сколько в первом и втором сосудах вместе. 379. Сумма 3986 + 5718 равна 9704. Пользуясь этим, найдите без вычислений значение выражения или корень уравнения: а) 9704 - 3986; г) 3986 + у = 9704;
380. Разность 6877 - 2984 равна 3893. Пользуясь этим, найдите без вычислений значение выражения или решите уравнение: а) 2984 + 3893; в) х - 3893 = 2984;
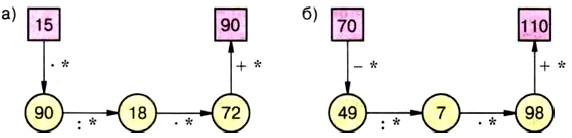
381. Вместо звёздочек в записи вычислений цепочкой поставьте необходимые числа.
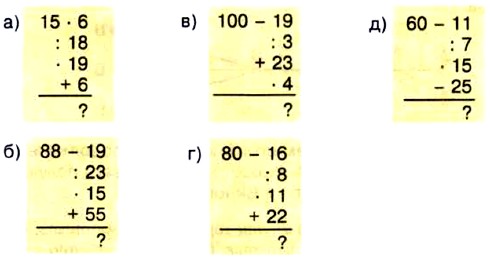
382. Вычислите устно:
383. На координатном луче даны точки A(18), В(7), С(31), D(27), Е(23), O(0). Какие из этих точек: а) левее точки Е и на сколько единичных отрезков;
384. Что больше и во сколько раз: а) два часа или сорок минут;
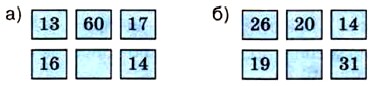
385. В бидоне 24 л молока. Для приготовления завтраков израсходовали четвёртую часть молока, а для приготовления обедов — половину оставшегося молока. Сколько литров молока осталось в бидоне? 386. Найдите пропущенное число:
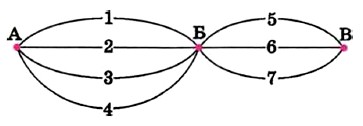
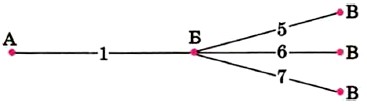
387. Вместо некоторых цифр поставлены звёздочки. Можно ли сравнить числа: а) 32** и 31**; б) *1** и 8**; в) **** и ***; г) *5* и 1**? 388. Из села Аникеево в село Большово ведут четыре дороги, а из села Большово в село Виноградово — три дороги. Сколькими способами можно добраться из Аникеева в Виноградово через село Большово?
Р е ш е н и е. Если из А в Б добираться по 1-й дороге, то продолжить путь есть три способа:
Точно так же рассуждая, получаем по три способа продолжить путь, начав добираться и по 2-й, и по 3-й, и по 4-й дороге. Значит, всего получается 4 • 3 = = 12 способов добраться из Аникеева в Виноградово.
|
|
|




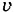 = 5718.
= 5718.