|
|
|
|
|
§ 4. Площади и объёмы 17. ФормулыЗадача 1. Велосипедист едет со скоростью 15 км/ч. Какое расстояние он проедет за 4 ч? Р е ш е н и е. Чтобы узнать, сколько километров проедет велосипедист, надо умножить его скорость на время пути, то есть найти произведение 15-4. Получаем, что путь равен 60 км.
Запишем правило нахождения пути по скорости и времени движения в буквенном виде. Обозначим путь буквой s, скорость — буквой
Запись какого-нибудь правила с помощью букв называют формулой. По формуле пути можно решать различные задачи.
Задача 2. Автомобиль движется со скоростью 60 км/ч. За какое время он пройдёт путь в 600 км? Р е ш е н и е. Заменим в формуле s = Задача 3. С какой скоростью должен идти человек, чтобы пройти 24 км за 4 ч? Р е ш е н и е. Заменим в формуле s =
674. Найдите по формуле s = а) со скоростью 96 м/мин за 25 мин;
675. Найдите по формуле пути значение скорости а) t= 12 ч, s = 240 км;
676. Найдите по формуле пути значение времени t, если: а) s = 64 км, 677. Запишите формулу для вычисления периметра прямоугольника, если буквами а и b обозначены длины сторон прямоугольника, а буквой Р его периметр. Вычислите по этой формуле: а) периметр Р прямоугольника, если его стороны а = 4 дм и b = 3 дм;
678. Запишите формулу для вычисления периметра Р квадрата, сторона которого а. Вычислите по этой формуле: а) периметр квадрата со стороной 9 см;
679. Запишите в виде формулы правило нахождения делимого а по делителю b, неполному частному g и остатку r. По этой формуле найдите: а) делимое а, если неполное частное равно 15, делитель — 7 и остаток — 4;
|
|
|




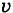 и время — буквой t. Получим равенство s =
и время — буквой t. Получим равенство s = 

