|
|
|
|
|
§ 1. Делимость чисел 1. Делители и кратные (окончание)
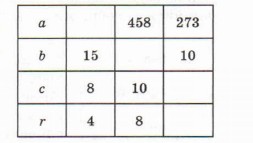
21. При делении числа а на число b получили неполное частное с и остаток г. С помощью формулы а = be + r заполните пустые клетки таблицы. 22. Выполните действие:
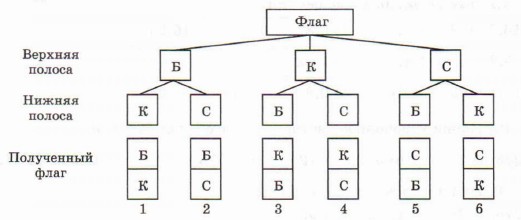
23. Государственные флаги многих стран состоят из горизонтальных или вертикальных полос разных цветов. Сколько могло бы быть различных государственных флагов, состоящих из двух горизонтальных полос одинаковой ширины и разного цвета — белого, красного и синего? Решение. Пусть верхняя полоса флага — белая (Б). Тогда нижняя полоса может быть красной (К) или синей (С). Получили две комбинации —два варианта флага. Если верхняя полоса флага — красная, то нижняя может быть белой или синей. Получили ещё два варианта флага. Пусть, наконец, верхняя полоса — синяя, тогда нижняя может быть белой или красной. Это ещё два варианта флага. Всего получили 3 - 2 = 6 комбинаций — шесть вариантов флага (см. схему).
Для решения этой задачи мы рассмотрели все возможные варианты расположения цветных полос на флаге, или все возможные комбинации. Такие задачи называют комбинаторными, а раздел математики, занимающийся подобными задачами, — комбинаторикой.
24. Сколько существует флагов, составленных из трёх горизонтальных полос одинаковой ширины и различных цветов — белого, зелёного, красного и синего? Есть ли среди этих флагов Государственный флаг Российской Федерации? 25. Решите задачу: 1) В первом мешке было 54,4 кг крупы, во втором — в 1,7 раза меньше, чем в первом, а в третьем — на 2,6 кг больше, чем во втором. Сколько килограммов крупы было в трёх мешках вместе? 2) На первую машину погрузили 4,5 т картофеля, на вторую — в 1,4 раза больше, чем на первую, а на третью — на 1,6 т меньше, чем на вторую. Сколько тонн картофеля погрузили на все три машины вместе? 26. Найдите все делители числа 30 и запишите их в порядке возрастания. 27. Выберите из чисел 14, 21, 31, 42, 51, 63, 68, 75 те, которые: а) кратны 7; б) кратны 17; в) не кратны 8; г) не кратны 2. 28. Выполните деление с остатком: 385 : 13; 548 : 12; 3710 : 30. 29. Площадь первого поля 27,3 га. Площадь второго поля на 4,8 га меньше площади первого, а площадь третьего поля в 1,6 раза больше площади второго. Чему равна площадь всех трёх полей вместе? 30. Выполните действия:
|
|
|