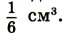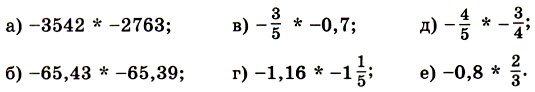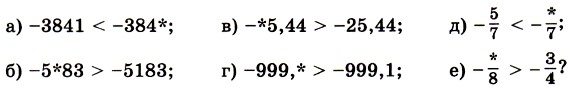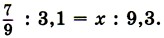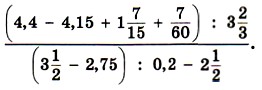|
|
|
|
|
§ 5. Положительные и отрицательные числа 29. Сравнение чисел (окончание)990. Определите, у какого из двух чисел модуль больше:
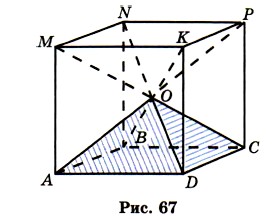
991. Из рисунка 67 видно, что куб можно составить из шести одинаковых четырёхугольных пирамид, у которых вершина О, а основаниями служат грани куба. Найдите объём пирамиды, если ребро куба 1,2 см. Найдите ребро куба, если объём одной пирамиды 992. Найдите неизвестный член пропорции: 1) 3,5 : x = 0,8 : 2,4; 2) 6,8 : 2,5 = x : 1,5. 993. Зешите задачу: 1) Для приготовления компота смешали 2,5 кг яблок, 2 кг груш и 0,5 кг вишен. Найдите процентное содержание каждого вида фруктов, взятых для приготовления компота. 2) Смешали 0,16 кг грузинского, 0,52 кг азербайджанского и 0,12 кг индийского чая. Найдите процентное содержание каждого вида чая в полученной смеси. 994. Вычислите: 1) 61,71 : ((14,42 - 13,74) • 1,5) + 63,163 : 7,61; 2) 73,32 : ((15,41 - 14,76) • 1,6) + 55,186 : 6,73. Проверьте результат вычислений с помощью микрокалькулятора. 995. Поставьте вместо * знак > или < так, чтобы получилось верное неравенство:
996. Какие цифры можно написать вместо *, чтобы получилось верное неравенство:
997. Расположите числа 2,8; 0,5; 0; -1; -1,1; 0,1 и -1,6: а) в порядке возрастания; б) в порядке убывания. 998. За контрольную работу 6 человек получили отметку «5», 10 человек — «4», а остальные четверо — «3». Сколько процентов всех учащихся получили отметку «5», сколько — «4» и сколько — «3»? 999. Найдите неизвестный член пропорции
1000. Вычислите:
|
|
|