|
|
|
|
|
Методы психодиагностики подростков и юношей Методы оценки мышления у подростков и старших школьников. Психодиагностика. НемовОтветы на задачи словесного субтеста теста Айзенка1. ГАЗ.
Ответы на задачи числового субтеста теста Айзенка и их объяснение1. 48. Сначала прибавляется 2, потом 4, затем 8 и, наконец, 16. 2. 24. Числа постепенно возрастают на 2,3,4,5,6 по направлению против часовой стрелки. 3. 80. Из каждого числа вычитаем 33. 4. 5. Цифры, поднятые на «руках», положительные, а цифры, находящиеся на опущенных «руках» — отрицательные. На «голове» дана их алгебраическая сумма: +7 - 2 = +5. 5. 18. Имеются два чередующихся ряда чисел. В одном ряду числа возрастают на 4, а в другом ряду — на 3. 6. 154. Это — удвоенная сумма чисел, стоящих вне скобок. 7. 3. Это — полуразность чисел второй и первой колонок. 8. 86. Числа удваиваются, а затем из них вычитаются 1,2,3,4. 9. 333. Это — разность чисел, стоящих справа и слева от скобок. 10. 35. Числа в ряду возрастают на 1, 2, 4,8,16. 11. 5. Число на «голове» равно полусумме чисел на «ногах». 12. 37. Каждое последующее число равно удвоенному предыдущему минус 5. 13. 7. Числа в третьей колонке равны полусумме чисел в первой и второй колонках. 14. 33. Числа в ряду убывают на 16, 8,4, 2,1. 15. 3. Если двигаться по часовой стрелке, то числа все время возрастают в три раза. 16. 14. Число в скобках равно сумме чисел вне скобок, деленной на 50. 17. 6. Имеются два чередующихся ряда чисел. В одном ряду числа уменьшаются на 3, а в другом ряду — на 2. 18. 4. Сумма чисел в каждой строке равна 14. 19.18. Каждое последующее число равно удвоенному предыдущему минус 10. 20. 3. Имеются три убывающих ряда чисел. В первой строке числа уменьшаются на 3, во второй строке — на 2, в третьей — на 3. 21. 18. Удвоенное число противоположного сектора. 22. Удвоенная разность чисел, стоящих справа и слева от скобок.- 23. 21. Числа возрастают на 2, 4, 6, 8. 24. 480. Число в скобках равно удвоенному произведению чисел, стоящих вне скобок. 25. 2. В каждой строке третье число равно удвоенной разности первых двух чисел. 26. 19. Имеются два чередующихся ряда чисел. В первом ряду числа возрастают на 3, 4, 5. Во втором ряду числа убывают на 2 и 3. 27. 3. Вычесть сумму чисел на второй и четвертой «лапах» из суммы чисел на первой и третьей «лапах». В результате получится число на кончике «хвоста». 28. 77. Число в скобках равно половине произведения чисел, стоящих вне скобок. 29. 7. Каждое последующее число равно половине предыдущего минус 2. 30. 61. Каждое последующее число равно сумме предыдущего с удвоенной разностью двух предшествующих. Так: 5 - 1 = 4; 4 х 2 = 8; 5 + 8 = 13 и т. д. 31. 11. Удвоить число из противолежащего сектора и прибавить к полученному результату 1. 32. 46. Каждое последующее число равно удвоенному предыдущему плюс 2. 33. 24. Числа в ряду возрастают на 3, 5, 7, 9. 34. 5. Имеются два чередующихся ряда чисел. В первом ряду числа увеличиваются на 2. Во втором ряду числа уменьшаются на 1. 35. 518. Число в скобках равно удвоенной разности чисел, стоящих вне скобок. 36. 3. Вычесть сумму чисел на «ногах» из суммы чисел на «руках». В результате получается число на «голове». 37. 19. Имеются два чередующихся ряда чисел. В одном ряду числа увеличиваются на 5, в другом ряду — на 4. 38. 152. Если двигаться по часовой стрелке, то каждое последующее число будет равно удвоенному предыдущему плюс 2, 3, 4, 5, 6. 39. 40. Числа во второй колонке равны удвоенным числам первой колонки плюс 2 : 2 х 19 + 2 = 40. 40. Числа в верхних квадратах увеличиваются на 3,4,5,7. Числа в нижних квадратах увеличиваются на 4, 5, 6, 7. 41. 66. Если двигаться по часовой стрелке, то каждое последующее число равно удвоенному предыдущему минус 2. 42.179. Если двигаться по часовой стрелке, то каждое последующее число равно удвоенному предыдущему плюс 1,3, 5,7,9. 43. 64. Возвести в квадрат число из противолежащего сектора. 44. 111. Число в скобках равно полуразности чисел, стоящих вне скобок. 45. 297. Разность между числами каждый раз удваивается, и ее нужно поочередно прибавлять и вычитать из чисел ряда, например: 857 + 112 = 969; 969 - 112 х 2 = 745; 745 + 112 х 2x2 = 1193; 1193 - 112 x 2 x 2 x 2 = 297. 46. 6. Имеются два чередующихся ряда чисел. Оба они представляют собой квадраты чисел плюс 2:
47. 55 и 100. Число, стоящее справа от скобок, равно квадрату числа, стоящего слева от скобок. Число в скобках равно полусумме чисел вне скобок. 48. 91. В приведенном ряду разность между каждым последующим числом и предыдущим возрастает на 6 и составляет, соответственно, 12,18, 24, 30. 49.
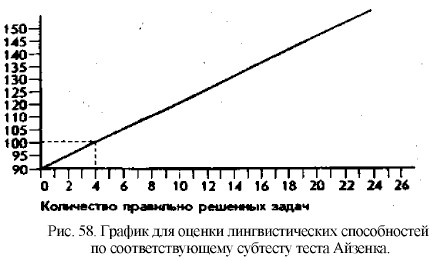
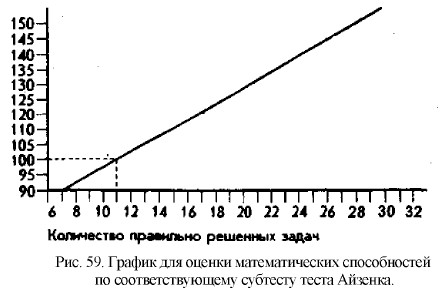
50. 6. Число внутри кружка равно сумме чисел внутри углов треугольника минус числа, стоящие вне треугольника. Оценка результатов исследования лингвистических и математических способностей (мышления) при помощи описанных субтестов теста АйзенкаОценка результатов исследования производится при помощи графиков, показанных на рис. 58 и рис. 59. Они представляют собой усредненные нормативные показатели по данным этих двух субтестов. Норме в строгом смысле этого слова на каждом графике соответствует показатель, равный 100% по вертикальной оси.
Найдя, пользуясь графиком, соответствующую точку на нижней оси (количество задач, правильно решенных испытуемым за 30 мин), восстановив из нее перпендикуляр до пересечения с линией графика и далее опустив его из точки пересечения на вертикальную ось, можно определить коэффициент интеллектуального развития испытуемого по данному виду мышления. Так, например, если за отведенные 30 мин испытуемый решил 16 задач, то показатель уровня развития его лингвистического мышления приблизительно будет равен 130%. Если за это же время такое же число задач решено по математическому субтесту, то показатель уровня развития математического мышления окажется равным 115%. Норме для лингвистического субтеста соответствуют 4 правильно решенные задачи, а норме для математического субтеста — 11 правильно решенных задач (пунктирные линии на обоих графиках).
|
|
|