|
|
|
|
|
Глава 5. Закон сохранения энергии
§ 40. Механическая работа и мощность силыЗакон сохранения энергии — фундаментальный закон природы, позволяющий описывать большинство происходящих явлений. Описание движения тел также возможно с помощью таких понятий динамики, как работа и энергия. Вспомните, что такое работа и мощность в физике. Совпадают ли эти понятия с бытовыми представлениями о них? Совершает ли учитель физики механическую работу во время урока? Если да, то в каких случаях?
Все наши ежедневные действия сводятся к тому, что мы с помощью мышц либо приводим в движение окружающие тела и поддерживаем это движение, либо же останавливаем движущиеся тела. Этими телами являются орудия труда (молоток, ручка, пила), в играх — мячи, шайбы, шахматные фигуры. На производстве и в сельском хозяйстве люди также приводят в движение орудия труда. Применение машин во много раз увеличивает производительность труда благодаря использованию в них двигателей. Назначение любого двигателя в том, чтобы приводить тела в движение и поддерживать это движение, несмотря на торможение как обычным трением, так и «рабочим» сопротивлением (резец должен не просто скользить по металлу, а, врезаясь в него, снимать стружку; плуг должен взрыхлять землю и т. д.). При этом на движущееся тело должна действовать со стороны двигателя сила. Работа совершается в природе всегда, когда на какое-либо тело в направлении его движения или против него действует сила (или несколько сил) со стороны другого тела (других тел).
Определение работы. Второй закон Ньютона в импульсной форме Δ
Изменение скорости по модулю возможно лишь в том случае, когда проекция силы Fr на направление перемещения тела отлична от нуля. Именно эта проекция определяет действие силы, изменяющей скорость тела по модулю. Она совершает работу. Поэтому работу можно рассматривать как произведение проекции силы Fr на модуль перемещения |Δ А = Fr|Δ Если угол между силой и перемещением обозначить через α, то Fr = Fcosα. Следовательно, работа равна: А = |Δ
В общем случае при движении твёрдого тела перемещения его разных точек различны, но при определении работы силы мы под Δ Работа, в отличие от силы и перемещения, является не векторной, а скалярной величиной. Она может быть положительной, отрицательной или равной нулю. Знак работы определяется знаком косинуса угла между силой и перемещением. Если α < 90°, то А > 0, так как косинус острых углов положителен. При α > 90° работа отрицательна, так как косинус тупых углов отрицателен. При α = 90° (сила перпендикулярна перемещению) работа не совершается. Если на тело действует несколько сил, то проекция равнодействующей силы на перемещение равна сумме проекций отдельных сил: Fr = F1r + F2r + ... . Поэтому для работы равнодействующей силы получаем А = F1r|Δ
|
Понаблюдайте за работой швейной или стиральной машины и найдите в ней устройство, заменяющее ручной труд.
Сила тяготения совершает работу при падении капель дождя или камня с обрыва. Одновременно совершает работу и сила сопротивления, действующая на падающие капли или на камень со стороны воздуха. Совершает работу и сила упругости, когда распрямляется согнутое ветром дерево.
= 
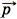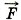Δt позволяет определить, как меняется скорость 
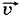тела по модулю и направлению, если на него в течение времени Δt действует сила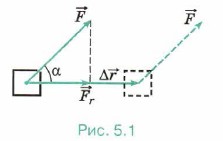 
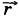| (рис. 5.1):
|
|