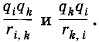|
|
|
|
|
Глава 1. Электростатика Потенциальная энергия заряда в однородном электрическом поле. Энергия взаимодействия точечных зарядовЭнергия взаимодействия точечных зарядовВ курсе механики было получено выражение для энергии взаимодействия точечных тел:
Если вместо точечных масс взять два разноименных по знаку заряда q1 и q2 (заряды притягиваются), то можно получить аналогичное выражение для потенциальной энергии их взаимодействия:
Для зарядов одного знака (заряды отталкиваются) знак потенциальной энергии будет противоположным:
Формулы (1.18.6) и (1.18.7) можно объединить в одну, если вместо модулей зарядов взять их алгебраические значения:
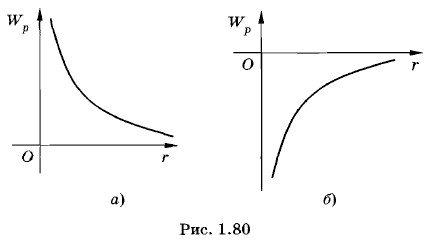
Знак потенциальной энергии автоматически получится правильным. Если заряды q1 и q2 имеют одинаковые знаки, то потенциальная энергия их взаимодействия положительна (рис. 1.80, а). Она тем больше, чем меньше расстояние между зарядами, так как работа, которую могут совершить кулоновские силы при отталкивании зарядов друг от друга, будет больше. Если заряды имеют противоположные знаки, то энергия отрицательна и максимальное ее значение, равное нулю, достигается при r → ∞ (рис. 1.80, б). Чем больше r, тем бо́льшую работу совершат силы притяжения при сближении зарядов.
При записи потенциальной энергии в форме (1.18.8) уже сделан определенный выбор нулевого уровня потенциальной энергии. Считается, что потенциальная энергия бесконечно удаленных зарядов равна нулю: Wp → 0 при r →. Такой выбор нулевого уровня удобен, но не обязателен. Вместо выражения (1.18.8) можно было бы с тем же успехом записать, что
где С — произвольная постоянная. Отсюда видно, что положительное или отрицательное значение потенциальной энергии особого физического смысла не имеет. Знак потенциальной энергии будет определенным при фиксации произвольной постоянной С. Изменив значение С, мы можем изменить знак W при данном расстоянии r между зарядами. Потенциальная энергия системы точечных зарядовПотенциальная энергия системы точечных зарядов q1, q2, ... ,qN равна сумме потенциальных энергий всех пар взаимодействующих зарядов. Для трех зарядов
Докажите это самостоятельно, используя следующий прием. Вначале заряды q2 и q3 находятся на бесконечно большом расстоянии от заряда q1. Затем заряд q2 перемещается в точку, находящуюся на расстоянии r1,2 от первого заряда. Вслед за тем заряд q3 перемещается в точку на расстоянии r1,3 от первого заряда и r2,3 от второго. Надо вычислить работу кулоновских сил, совершаемую при этих перемещениях, и приравнять ее изменению потенциальной энергии, взятому с противоположным знаком. В общем случае N зарядов
где ri k — расстояние между зарядами номеров i и k. Коэффициент
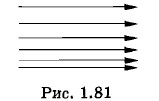
1. Можно ли создать электростатическое поле, линии напряженности которого параллельны, а модуль напряженности возрастает в направлении, перпендикулярном линиям (рис. 1.81)? 2. Нарисуйте график зависимости потенциальной энергии разноименно заряженных частиц от расстояния при условии, что произвольная постоянная С в формуле (1.18.9) положительна. 3. Как будет выглядеть формула (1.18.8), если заряды находятся в среде с диэлектрической проницаемостью ε?
|
|
|



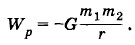




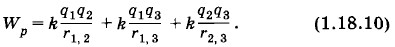
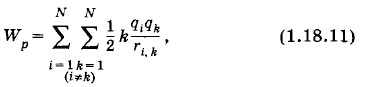
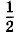 получается из-за того, что при суммировании потенциальная энергия учитывается дважды в виде одинаковых слагаемых
получается из-за того, что при суммировании потенциальная энергия учитывается дважды в виде одинаковых слагаемых