|
|
|
|
|
Глава 1. Электростатика § 1.19. Потенциал электростатического поля и разность потенциалов
ПотенциалПотенциальная энергия заряда в электростатическом поле пропорциональна самому заряду. Это справедливо как для однородного поля, так и для любого другого. В частности, потенциальная энергия заряда q2 в поле точечного заряда q1 пропорциональна, согласно формуле (1.18.8), заряду q2. Следовательно, отношение потенциальной энергии к заряду не зависит от помещенного в поле заряда. Это позволяет ввести новую количественную характеристику электростатического поля — потенциал, не зависящую от помещенного в поле заряда. Потенциалом электростатического поля называется отношение потенциальной энергии заряда в поле к этому заряду. Обозначим потенциал буквой φ. Тогда по определению
Напряженность поля Потенциал однородного поляЕсли в качестве нулевого уровня потенциальной энергии, а значит, и потенциала, принять потенциал положительно заряженной пластины В (см. рис. 1.79), то, согласно формулам (1.18.3) и (1.19.1), потенциал однородного поля равен:
Потенциал однородного поля является линейной функцией координаты. Потенциал поля точечного заряда Потенциал поля точечного зарядаПотенциальная энергия заряда q0, находящегося в поле точечного заряда q, согласно формуле (1.18.8), равна:
Отсюда в соответствии с определением потенциала (1.19.1) потенциал точечного заряда равен:
В этом выражении потенциал на бесконечности (r → ∞) выбран нулевым, поэтому при q > 0 φ > 0, а при q < 0 φ < 0. Формула (1.19.4) справедлива также и для потенциала поля равномерно заряженной сферы (или равномерно заряженного шара) на расстояниях, бо́льших или равных ее радиусу, так как поле сферы (или шара) вне сферы и на ее поверхности совпадает с полем точечного заряда, помещенного в центре сферы. Потенциал поля произвольной системы зарядовЗаряд любого тела (или нескольких тел) можно мысленно разделить на столь малые элементы, что каждый из них будет представлять собой точечный заряд. Тогда потенциал в произвольной точке определится как алгебраическая сумма потенциалов φ1, φ2, φ3, ..., создаваемых отдельными точечными зарядами: φ = φ1 + φ2 + φ3 +... . (1.19.5) Это соотношение является следствием принципа суперпозиции полей.
|
|
|




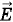 является вектором и представляет собой силовую характеристику поля; она определяет силу, действующую на заряд q в данной точке поля. Потенциал φ — скаляр. Это энергетическая характеристика поля. Он определяет потенциальную энергию заряда q в данной точке поля.
является вектором и представляет собой силовую характеристику поля; она определяет силу, действующую на заряд q в данной точке поля. Потенциал φ — скаляр. Это энергетическая характеристика поля. Он определяет потенциальную энергию заряда q в данной точке поля.


