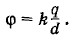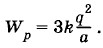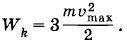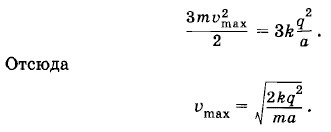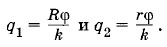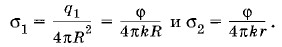|
|
|
|
|
Глава 1. Электростатика § 1.23. Примеры решения задачВ этом параграфе рассматриваются задачи с использованием понятий потенциальной энергии, потенциала и разности потенциалов. Работа сил, действующих на заряд со стороны электростатического поля, выражается через разность потенциальных энергий или разность потенциалов [см. формулы (1.17.1) и (1.19.6)]. Потенциал точечного заряда определяется формулой (1.19.4), а потенциал однородного поля формулой (1.19.2). Кроме того, надо знать выражение (1.18.8) для энергии взаимодействия точечных зарядов и связь между напряженностью электрического поля и разностью потенциалов [формула (1.20.4)]. При решении задач на движение заряженных частиц в электрическом поле можно использовать законы сохранения энергии и импульса, а также законы механики Ньютона. Задача 1На расстоянии d от точечного заряда q расположен центр незаряженного проводящего шара радиусом R. Чему равен потенциал шара? Решение. Потенциал всех точек шара одинаков, поэтому достаточно найти потенциал одной точки. Проще всего найти потенциал центра шара. Он равен сумме потенциала, созданного в центре шара точечным зарядом
Задача 2Три заряженных одинаковых шарика, заряд каждого из которых равен q, а масса — m, расположены в вершинах равностороннего треугольника со стороной a. Каких максимальных скоростей достигнут шарики, отталкиваясь друг от друга, если их отпустить? Решение. В начальном состоянии шарики обладают потенциальной энергией:
Разлетаясь, шарики вследствие симметрии будут иметь одинаковые по модулю скорости. Эти скорости максимальны на бесконечности, где Wp = 0, a Согласно закону сохранения энергии
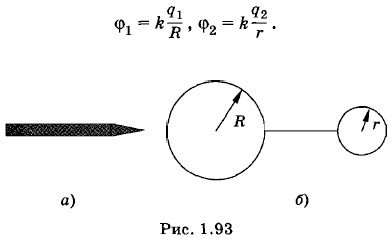
Задача 3Почему на проводниках, имеющих форму острия, поверхностная плотность заряда достигает значительных величин? Решение. На рисунке 1.93, (а) изображен проводник, имеющий форму острия. Моделью острия может служить (в первом приближении) система двух шаров различных радиусов, соединенных тонкой проволокой (рис. 1.93, б). Радиус левого шара R значительно больше радиуса правого шара r (R » r). Пренебрегая влиянием шаров друг на друга, их потенциалы можно записать в виде:
Так как шары соединены проводником, то φ1 = φ2 = φ. Следовательно,
Поверхностные плотности заряда шаров соответственно равны:
Так как R » r, то σ2 » σ1, т. е. поверхностная плотность заряда на малом шаре, кривизна которого велика (на острие), значительно больше поверхностной плотности заряда на большом шаре, кривизна которого мала.
|
|
|



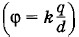 и потенциала, созданного зарядами, возникающими на поверхности шара вследствие электростатической индукции. Но этот потенциал равен нулю, так как суммарный заряд на сфере равен нулю, и все элементы заряда находятся на равном расстоянии от центра. Следовательно, потенциал шара
и потенциала, созданного зарядами, возникающими на поверхности шара вследствие электростатической индукции. Но этот потенциал равен нулю, так как суммарный заряд на сфере равен нулю, и все элементы заряда находятся на равном расстоянии от центра. Следовательно, потенциал шара