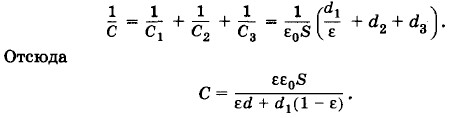|
|
|
|
|
Глава 1. Электростатика § 1.28. Примеры решения задачЭлектрическая емкость — последняя тема главы «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: сохранение электрического заряда, понятия напряженности поля и потенциала, поведение проводников в электростатическом поле, изменение напряженности поля в диэлектриках, закон сохранения энергии применительно к электростатическим явлениям. Только при хорошем усвоении всех основных понятий электростатики решение задач на электрическую емкость не вызовет особых затруднений. Основными формулами при решении задач на емкость являются следующие: формула (1.24.2) — определение емкости, формула (1.24.3) — емкость уединенного шара, выражения для емкости плоского конденсатора (1.25.3) и сферического конденсатора (1.25.7), а также формулы для определения емкости батареи конденсаторов при последовательном и параллельном их соединении (1.26.4) и (1.26.2). Надо знать еще формулы (1.27.3) и (1.27.9) для энергии заряженного конденсатора и заряженного уединенного тела. Два одинаковых металлических шарика радиусом г расположены в вакууме на расстоянии d друг от друга, причем d » r. Шарики заряжены одинаковыми по модулю и противоположными по знаку зарядами. Какова электрическая емкость системы, образованной шариками? Решение. Искомая емкость равна отношению заряда q одного из шариков к разности потенциалов между ними:
Найдем U. Потенциал φ1 первого шарика, несущего заряд +q, складывается из его собственного потенциала
Поскольку d » r, то с большой степенью точности можно считать, что
Задача 2
Найдите емкость С конденсатора, площадь пластин которого S и расстояние между ними l, если в конденсатор вставлена металлическая пластина толщиной d, параллельная его обкладкам (рис. 1.107). Решение. Конденсатор со вставленной в него пластиной можно рассматривать как два последовательно соединенных конденсатора. Емкость первого из них
Емкость не зависит от положения пластины. При очень тонкой пластине (d → 0) емкость конденсатора не зависит от наличия пластины. Задача 3В плоский конденсатор с расстоянием d между обкладками вводится диэлектрическая пластина, толщина которой d1 < d. Определите емкость конденсатора с диэлектрической пластиной. Диэлектрическая проницаемость материала пластины ε. Площадь пластины и каждой обкладки конденсатора S.
Решение. Если в плоский конденсатор внести очень тонкую проводящую пластину, параллельную обкладкам, то на ее поверхностях появятся заряды противоположных знаков, равные по модулю. При этом емкость конденсатора не изменяется (см. задачу 2). Поэтому можно считать, что на поверхностях диэлектрической пластины нанесены тонкие проводящие слои. В этом случае образуются три последовательно соединенных конденсатора с емкостями
|
|
|



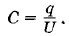
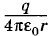 и потенциала в поле второго шарика, равного
и потенциала в поле второго шарика, равного 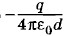 (см. задачу 16 § 1.23). Следовательно,
(см. задачу 16 § 1.23). Следовательно,
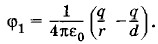
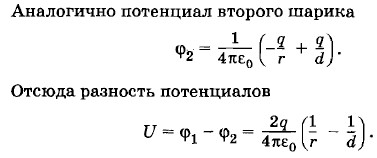
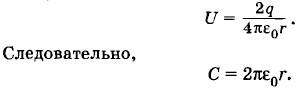
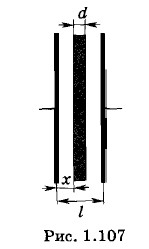
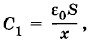 где х — расстояние от одной из обкладок до пластины. Емкость второго конденсатора
где х — расстояние от одной из обкладок до пластины. Емкость второго конденсатора 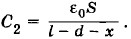 При последовательном соединении электрическая емкость батареи определяется уравнением:
При последовательном соединении электрическая емкость батареи определяется уравнением:
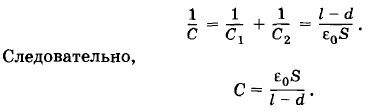
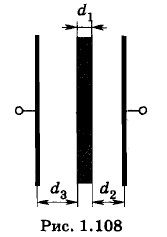
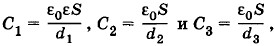 где d2 и d3 — расстояния между поверхностями диэлектрической пластины и обкладками, причем d2 + d3 = d - d1 (рис. 1.108). Емкость С батареи из трех конденсаторов определяется из формулы
где d2 и d3 — расстояния между поверхностями диэлектрической пластины и обкладками, причем d2 + d3 = d - d1 (рис. 1.108). Емкость С батареи из трех конденсаторов определяется из формулы