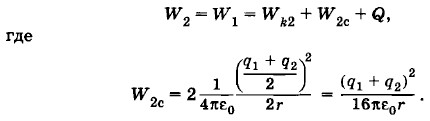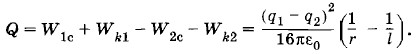|
|
|
|
|
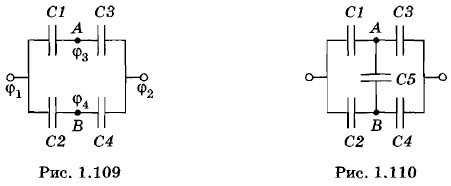
Глава 1. Электростатика § 1.28. Примеры решения задач (окончание)Задача 4На рисунке 1.109 изображена батарея конденсаторов. Их емкости равны С1 = С, С2 = 2С, С3 = ЗС, С4 = 6С. Изменится ли емкость батареи, если между точками А и В включить конденсатор с емкостью С5 = 8С? Решение. Обозначим потенциалы на зажимах батареи φ1 и φ2, а в точках А и В соответственно φ3 и φ4.
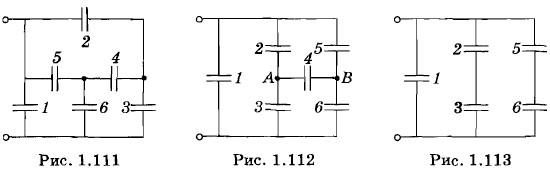
Так как конденсаторы C1 и СЗ соединены последовательно, то их заряды одинаковы, т. е. C1(φ1 - φ3) = С3(φ3 - φ2). (1.28.1) Аналогично С2(φ1 - φ4) = С(φ4 - φ2). (1.28.2) Разделив почленно равенство (1.28.1) на равенство (1.28.2) и учитывая, что, согласно условию задачи,
Отсюда найдем, что φ3 = φ4, т. е. точки А и В имеют одинаковые потенциалы. Поэтому если включить какой-либо конденсатор между точками А и В (рис. 1.110), то он не зарядится и, следовательно, не повлияет на емкость системы. Схема, подобная схеме, изображенной на рисунке 1.110, называется мостовой. Конденсаторы С1 и С2, СЗ и С4 называются плечами моста. Обратите внимание, что если емкости плеч моста пропорциональны Задача 5Найдите емкость батареи конденсаторов, изображенной на рисунке 1.111. Емкость каждого конденсатора равна С.
Решение. Данная схема соединения конденсаторов эквивалентна схеме, изображенной на рисунке 1.112. В этом можно убедиться, проверив, что каждый из конденсаторов соединен с источником и с другими конденсаторами точно так же, как в исходной схеме. Вследствие равенства емкостей всех конденсаторов разность потенциалов между точками А и В равна нулю. Поэтому конденсатор 4 можно исключить (см. задачу 4). В результате получится схема, изображенная на рисунке 1.113. Она состоит из трех параллельных ветвей, две из которых содержат по два последовательно включенных конденсатора. Общая емкость системы
Задача 6Два маленьких шарика радиусом r несут заряды q1 и q2, различные по модулю, но одинаковые по знаку. Шарики первоначально находятся на расстоянии l друг от друга. Один из шариков закреплен. Второй шарик, удаляясь под действием электростатических сил, приобретает максимальную кинетическую энергию Wk1. Если перед началом движения второго шарика оба шарика на некоторое время были соединены проводником, то второй шарик, удаляясь, приобретает максимальную кинетическую энергию Wk2 > Wk1. Определите количество теплоты, выделившееся в проводнике при соединении шариков, и выясните, за счет какой энергии выделяется эта теплота и увеличивается кинетическая энергия второго шарика. Решение. Согласно закрну сохранения энергии в первом случае Wk01 + Wp01 + W0c = Wk1 + Wp1 + W1c, где Wk01 и Wp01 + W0c — начальные, a Wk1 и Wp1 + W1c — конечные значения кинетической и потенциальной энергий системы двух шариков. Причем WpQ1 и Wp1 — потенциальные энергии взаимодействия шариков, a Wp01 и W1c — их суммарные собственные энергии, одинаковые по модулю. Считая потенциальную энергию взаимодействия при бесконечно большом расстоянии между шариками равной нулю и учитывая, что Wk01 = 0, получим:
После соединения проводником заряды шариков становятся одинаковыми и равными
Нетрудно видеть, что действительно Wk2 > Wk1 Кроме того, в проводнике выделяется количество теплоты Q. Однако, разумеется, полная энергия должна сохраняться. Увеличение кинетической энергии и выделение теплоты во втором случае происходит за счет уменьшения собственной потенциальной энергии заряженных шариков при их соединении. С учетом собственной энергии шариков конечную энергию в первом случае можно представить в виде W1 = Wk1 + W1c где
Количество выделенной теплоты равно:
|
|
|



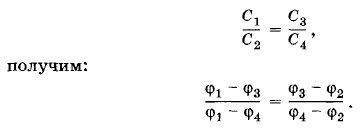
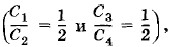 то точки А и В имеют одинаковые потенциалы. Конденсатор С5 не заряжается, и его из схемы можно удалить (см. рис. 1.109).
то точки А и В имеют одинаковые потенциалы. Конденсатор С5 не заряжается, и его из схемы можно удалить (см. рис. 1.109).
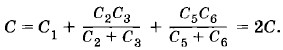
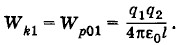
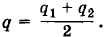 Начальная потенциальная энергия шариков изменяется. Кинетическая энергия второго шарика на бесконечности теперь равна:
Начальная потенциальная энергия шариков изменяется. Кинетическая энергия второго шарика на бесконечности теперь равна:
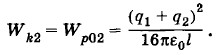
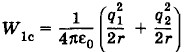 — собственная энергия шариков. Конечную энергию во втором случае запишем так:
— собственная энергия шариков. Конечную энергию во втором случае запишем так: