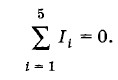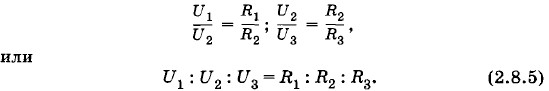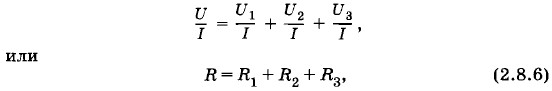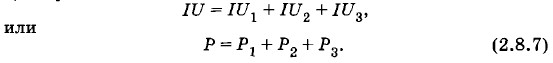§ 2.8. Электрические цепи. Последовательное и параллельное соединения проводников

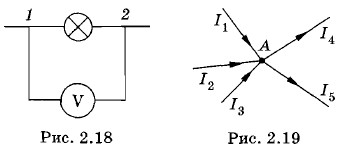
Энергия передается от источника тока к потребителям (лампам, электродвигателям, радиоприемникам и т. д.) по проводам. Источник тока, потребители энергии (их может быть, как правило, несколько), соединительные провода и выключатели для включения или выключения потребителей энергии образуют электрическую цепь. Часто в электрическую цепь включают приборы, контролирующие силу тока и напряжение на различных участках цепи, — амперметры и вольтметры. Все элементы электрической цепи определенным образом соединяют между собой. На практике проводники чаще всего соединяют последовательно или параллельно.

Разветвление токов

Очень часто в электрических цепях в одной точке сходятся несколько (больше двух) проводников. Например, при включении вольтметра для измерения напряжения на зажимах лампы (рис. 2.18) в точках 1 и 2 сходятся по три проводника. Такие точки называются точками разветвления или узлами.

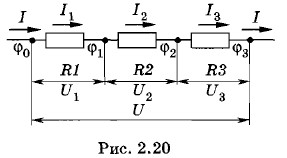
На рисунке 2.19 в точке разветвления А сходятся пять проводников. Обозначим силу тока в них I₁, I₂, I₃, I₄ и I₅. Из рисунка видно, что токи I₁, I₂, I₃ направлены к узлу и за произвольный промежуток времени At приносят в этот узел суммарный заряд (I₁ + I₂ + I₃) Δt. Токи I₄ и I₅ направлены от узла и уносят за это же время заряд (I₄ + I₅) Δt. Полное изменение заряда в узле за промежуток времени Δt равно:

Δq = (I₁ + I₂ + I₃)Δt - (I₄ + I₅)Δt = (I₁ +I₂ + I₃ - I₄ - I₅)Δt

В цепи постоянного тока потенциалы всех точек цепи, а значит, и узлов, должны оставаться неизменными. Следовательно, в этих узлах не могут накапливаться электрические заряды ни положительного, ни отрицательного знака. В частности, для узла А изменение заряда Δq должно равняться нулю для любого интервала времени, т. е.

I₁ +I₂ + I₃ - I₄ - I₅ = 0. (2.8.1)

Рассматривая силу тока как алгебраическую величину, имеющую знак «плюс», если ток подходит к узлу, и знак «минус», если ток направлен от узла, последнее равенство можно записать так:

Если в узле сходятся N токов, то

Это равенство называется первым правилом Кирхгофа: алгебраическая сумма сил токов в проводниках, сходящихся в узле, равна нулю.

Последовательное соединение проводников

Последовательным соединением проводников называется такое их соединение, при котором конец первого проводника соединяется с началом второго, конец второго — с началом третьего и т. д. На рисунке 2.20 показано последовательное соединение трех проводников, имеющих сопротивления R₁, R₂, R₃.

При последовательном соединении проводников выполняется ряд простых соотношений.

1. Сила тока во всех последовательно соединенных проводниках одинакова:

I₁ = I₂ = I₃ = I (2.8.3)

2. Напряжение (или разность потенциалов) на концах рассматриваемого участка цепи равно сумме напряжений на отдельных проводниках:

U = U₁ + U₂ + U₃. (2.8.4)

Действительно: U1 = φ₀ — φ₁; U₂ = φ₁ - φ₂ и U₃ = φ₂ - φ₃. Складывая U₁, U₂ и U₃ получим φ₀ - φ₃ = U.

В справедливости равенства (2.8.4) можно убедиться и непосредственным измерением при помощи вольтметра напряжений на всем участке цепи и на отдельных проводниках.

3. Согласно закону Ома напряжения на отдельных проводниках равны: U₁ = IR₁; U₂ = IR₂; U₃ = IR₃.

Отсюда следует, что

При последовательном соединении напряжения на проводниках пропорциональны их сопротивлениям.

4. Разделив равенство (2.8.4) почленно на силу тока I, получим:

где R — сопротивление всего рассматриваемого участка цепи.

Таким образом, сопротивление участка цепи, состоящего из нескольких последовательно соединенных проводников (общее сопротивление), равно сумме сопротивлений отдельных проводников.

5. Умножив теперь все члены равенства (2.8.4) на силу тока I, получим:

Мощность тока на всем участке цепи равна сумме мощностей тока на отдельных последовательно соединенных проводниках.

Все изложенные выше выводы справедливы не только для трех, но и для любого числа последовательно соединенных проводников.

Окончание параграфа >>>