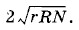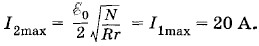|
|
|
|
|
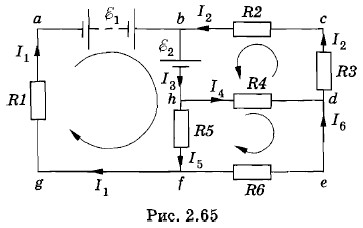
Глава 2. Постоянный электрический ток § 2.18. Примеры решения задач (окончание)Задача 6Найдите силы токов в каждой ветви электрической цепи, схема которой показана на рисунке 2.65. Решение. Зададим произвольно направления токов (см. рис. 2.65). Применим первое правило Кирхгофа для узлов b, h и f (для упрощения записей модули сил токов обозначим буквами I1, I2, I3 и т. д.):
Теперь применим второе правило Кирхгофа для контуров. Выберем произвольно направление обхода контуров: контура abƒg — по часовой стрелке; контура bcdh — против часовой стрелки и контура hdeƒ — по часовой стрелке (и здесь для упрощения записей модули ЭДС источников обозначим буквами
Учитывая, что R1 = R2 = R3 = R4 = R5 = R6 = R, получим в итоге следующую систему уравнений:
Решение такой системы уравнений требует терпения и внимательности. Решим эту систему последовательным исключением неизвестных величин. Из последнего уравнения системы (2.18.6) находим I5 = I3 - I4. Подставив значение I5 в третье уравнение, получим систему:
Из третьего уравнения системы (2.18.8) находим
Из первого уравнения следует: I3 = I1 + I2. После подстановки значения тока I3 во второе и третье уравнения получаем:
Наконец, из второго уравнения находим
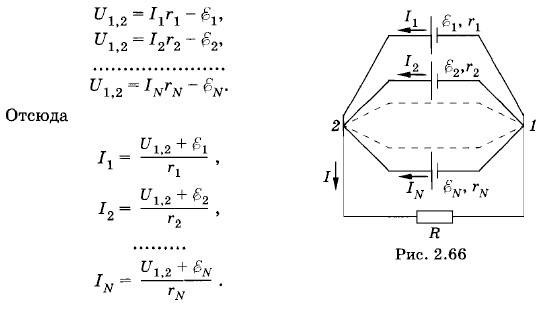
Отрицательные значения сил токов I2, I4 и I6 означают, что при данных значениях ЭДС и сопротивлений эти токи имеют направления, противоположные указанным на рисунке. Задача 7Батарея состоит из N параллельно соединенных источников тока (рис. 2.66). Определите ЭДС и внутреннее сопротивление источника тока, эквивалентного этой батарее. Решение. Обозначим ЭДС параллельно соединенных источников через Применив закон Ома (2.15.3) для участка цепи, содержащего ЭДС, для каждой ветви (см. рис. 2.66), получим:
Согласно первому правилу Кирхгофа
Пусть
Сравнивая выражения (2.18.11) и (2.18.12), видим, что
Таким образом, при параллельном соединении нескольких источников тока полученную батарею можно заменить эквивалентным источником тока, ЭДС которого ε и внутреннее сопротивление r можно найти из формул (2.18.13) и (2.18.14). Если все источники тока одинаковы и соединены одноименными полюсами, то из формул (2.18.13) и (2.18.14) следует, что
где Задача 8Можно ли с помощью 24 аккумуляторов, каждый из которых имеет ЭДС Решение. Возможны два способа соединения аккумуляторов. Можно внутри отдельных групп соединить аккумуляторы последовательно, а сами группы — параллельно, или же, наоборот, внутри группы — параллельно, а сами группы — последовательно. Обозначим через N полное число аккумуляторов, а через n — число аккумуляторов внутри отдельной группы. Тогда в первом случае сила тока равна:
так как ЭДС одной группы равна n Сила тока I1 достигнет максимума, когда значение знаменателя Для нахождения минимума выражения
Это выражение минимально при
Осуществив такие же преобразования , как и в первом случае, найдем, что сила тока достигает максимума при
Таким образом, получить во внешней цепи силу тока, превышающую 20 А, невозможно.
|
|
|



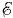 1 = 6,5 В;
1 = 6,5 В; 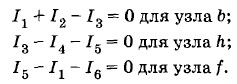
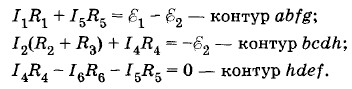
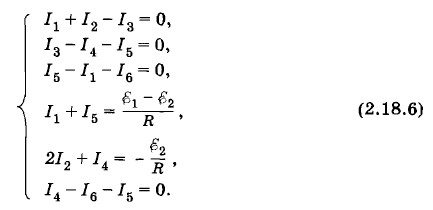
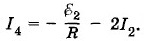 Подставив это значение тока во второе и четвертое уравнения, получим систему:
Подставив это значение тока во второе и четвертое уравнения, получим систему:
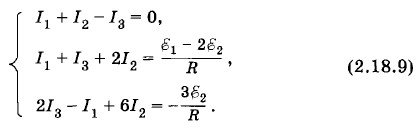
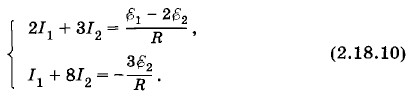
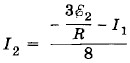 и подставляем в первое уравнение. Это дает
и подставляем в первое уравнение. Это дает
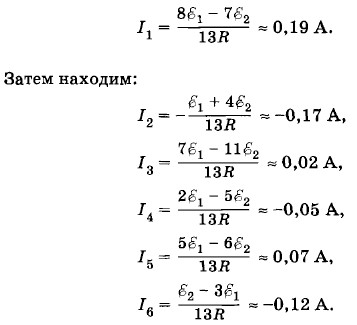
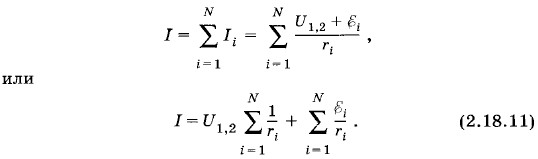
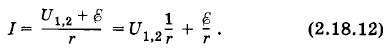
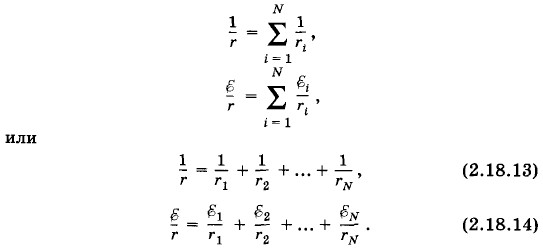

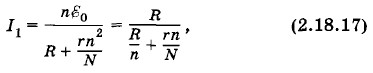
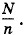
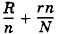 будет минимальным.
будет минимальным.
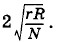 Получим:
Получим:
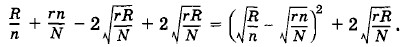
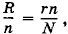 т. е. при
т. е. при 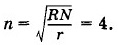 Оно равно
Оно равно 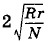 (выражение в скобках равно нулю). Следовательно,
(выражение в скобках равно нулю). Следовательно,
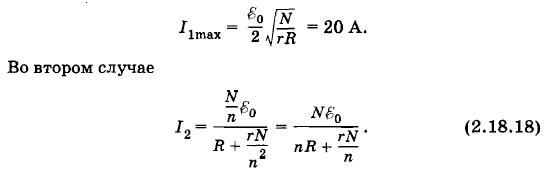
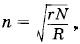 когда знаменатель выражения (2.18.18) имеет минимальное значение, равное
когда знаменатель выражения (2.18.18) имеет минимальное значение, равное