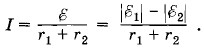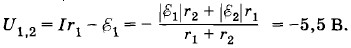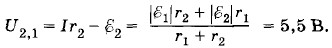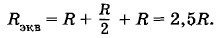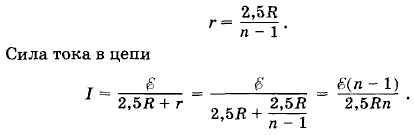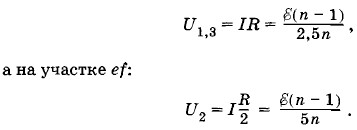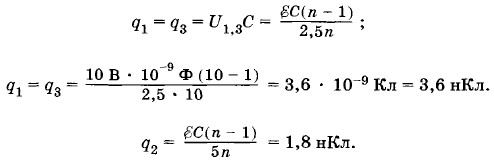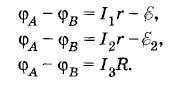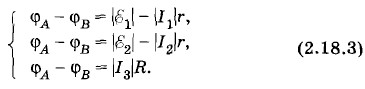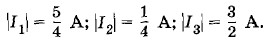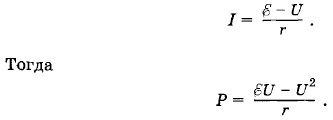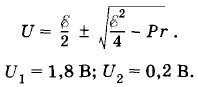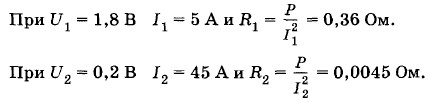|
|
|
|
|
Глава 2. Постоянный электрический ток § 2.18. Примеры решения задачПри решении задач на материал §2.11—2.17 надо, кроме формул предыдущих параграфов главы, применять закон Ома для полной цепи (2.14.5), закон Ома для участка цепи, содержащего ЭДС (2.15.3), правила Кирхгофа (2.8.2) и (2.17.4). Еще раз обращаем внимание на необходимость четкого знания правил определения знаков ЭДС, силы тока и напряжения (см. § 2.15). Задача 1
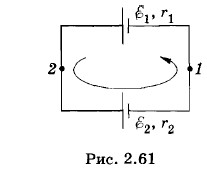
Два элемента, электродвижущие силы которых Решение. Условимся считать положительным направление обхода против часовой стрелки. Полная ЭДС цепи равна
Закон Ома для верхнего участка цепи между точками 1 и 2 запишется в виде:
Знак минус указывает на то, что потенциал точки 1 меньше потенциала точки 2. Тот же результат можно получить, применяя закон Ома к нижнему участку цепи:
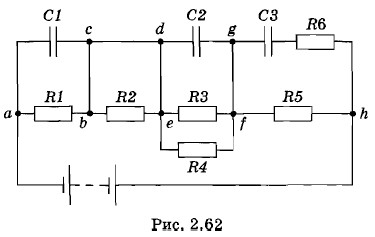
Задача 2В электрической цепи, схема которой изображена на рисунке 2.62, ЭДС батареи элементов
Решение. Из схемы видно, что ток не пойдет через резистор R2 (он закорочен проводником) и R6 (ветвь gh разомкнута конденсатором СЗ, так как постоянный ток через конденсатор не проходит). Поэтому эти резисторы можно исключить. Ток пойдет по цепи abcdeƒh. Эквивалентное внешнее сопротивление
Согласно закону Ома для полной цепи ЭДС батареи,
где r — внутреннее сопротивление батареи. При коротком замыкании
В соответствии с условием Iк.зr = In. Приравнивая правые части равенств (2.18.1) и (2.18.2), получим: I(r + 2,5R) = IRк.зr = Inr. Отсюда
Разность потенциалов на участках аb и ƒh одна и та же, она равна:
Заряды на обкладках конденсаторов С1,С2 и СЗ найдем так:
Задача 3Изобразите графически примерный ход потенциала вдоль замкнутой цепи с гальваническим элементом (элементом Даниэля), изображенной на рисунке 2.57. Решение. Если цепь разомкнута, то сила тока и падение напряжения во внешней цепи и внутри источника равны нулю. На границах электрод — раствор электролита в источнике существуют скачки потенциалов |U1| и |U2| (см. рис. 2.51). Сумма этих скачков равна ЭДС элемента:
При замыкании цепи скачки потенциалов на границах электрод — раствор электролита не изменяются. Но потенциал раствора электролита теперь не остается постоянным, а уменьшается в направлении тока, т. е. от отрицательного электрода к положительному. Падение напряжения на внутреннем сопротивлении U0 = Ir.
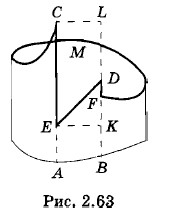
На рисунке 2.63 приведен примерный график распределения потенциала в замкнутой цепи. Отрезок АС изображает погенциал положительного электрода относительно некоторого произвольно выбранного пулевого уровня. Отрезок BF соответствует потенциалу отрицательного электрода. Расстояние между электродами равно АВ. Отрезки АЕ и BD — потенциалы раствора электролита вблизи положительного и отрицательного электродов. Наклонная линия DE изображает падение потенциала внутри элемента. Его значение U0 представлено отрезком DK. Кривая CMF дает представление о падении потенциала во внешней цепи на сопротивлении R. Это падение напряжения U = IR изображается отрезком LF. Отрезки СЕ = LK = |U2| и DF = |U1| соответствуют скачкам потенциала на границах электрод — раствор электролита. Линия CMFDEC, изображающая ход потенциала во всей цепи, является замкнутой. Это означает равенство нулю полной работы электростатического поля на замкнутом пути. Действительно, поле совершает положительную работу на участках CMF и DE и отрицательную — в тех местах, где имеются скачки потенциала вверх (FD и ЕС). По модулю положительная работа равна отрицательной. При перемещении единичного положительного заряда вдоль цепи положительная работа численно равна U0 + U = DK + LF, а отрицательная работа численно равна |U2| + |U2| = Может возникнуть вопрос: за счет чего же происходит выделение теплоты в цепи? На всех участках, кроме границ электрод — раствор электролита, действуют лишь электростатические силы. На границах, где есть скачки потенциала, действуют еще и сторонние (в данном случае химические) силы, причем отрицательная работа электростатических сил по модулю равна положительной работе сторонних сил. Поэтому положительная работа электростатических сил во всей остальной части цепи оказывается нескомпенсированной. За счет этой работы и происходит выделение теплоты. Рисунок 2.63 позволяет наглядно истолковать закон Ома для участка цепи, содержащего ЭДС. Как видно из рисунка, модуль напряжения |U| = LF = LK - FK = LK - (DK - DF) = (LK + DF) - DK = | Задача 4
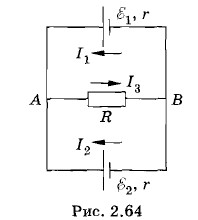
Два элемента, электродвижущие силы которых Решение. Зададим произвольно направление токов (см. рис. 2.64)*. * Если после решения задачи получится отрицательное значение силы тока, то это будет означать, что направление тока выбрано неправильно. Тогда на основании закона Ома для трех участков АВ (А — начало каждого участка, В — его конец) можно записать следующие уравнения:
При выбранном направлении от А к В (с учетом выбора направления токов) имеем:
Согласно первому правилу Кирхгофа для узла А имеем: |I1| + |I2| = |I3| Решая систему уравнений (2.18.3), с учетом предыдущего равенства находим искомые значения для модулей сил токов:
Задача 5Аккумулятор, ЭДС которого 2 В и внутреннее сопротивление r = 0,04 Ом, замкнут на резистор (см. рис. 2.57). Мощность тока, выделяемая на резисторе, Р = 9 Вт. Определите напряжение на клеммах аккумулятора. Решение. Мощность, выделяемая на резисторе, равна Р = IU. Согласно закону Ома (2.15.3) U1,2 = Ir - При выбранном направлении обхода (см. рис. 2.57) против часовой стрелки I > 0, -U1,2 = Но -U1,2 = U1,2 = U, где U — модуль напряжения на резисторе. Следовательно, U = Отсюда
Решая это квадратное уравнение относительно U, найдем:
Неоднозначность результата связана с тем, что одна и та же мощность тока может быть выделена при различных значениях сопротивления резистора, причем каждому значению сопротивления R соответствует своя сила тока.
|
|
|



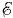 1 = 6 В и
1 = 6 В и