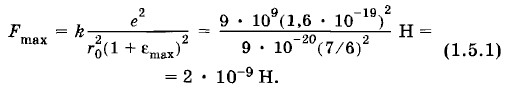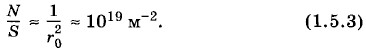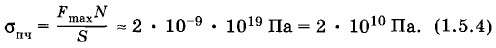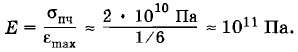|
|
|
|
|
Глава 1. Электростатика § 1.5. Оценка предела прочности и модуля Юнга ионных кристаллов
С помощью закона Кулона можно количественно оценить механические свойства ионных кристаллов: определить предел прочности кристаллов и вычислить (приближенно) модуль Юнга. В механике эти величины определяются экспериментально. Сила взаимодействия двух ионовРассмотрим ионный кристалл поваренной соли NaCl. Равновесное расстояние между соседними ионами в кристалле r0 ≈ 3 • 10-10 м (рис. 1.7).
Эксперименты с наиболее прочными кристаллами показывают, что их максимальная относительная деформация растяжения перед разрушением не превышает 10—20%. Будем считать максимальную относительную деформацию Заряд каждого иона по модулю равен элементарному заряду е. Согласно закону Кулона сила взаимодействия двух ионов на расстоянии г равна:
Таково по порядку величины максимальное значение силы межионной связи. Прочность кристалла при растяженииПри растяжении образца предел прочности определяется максимальным значением результирующей силы межионного притяжения, приходящейся на элемент сечения единичной площади, перпендикулярный направлению растяжения. Если на поверхности площадью S имеется N связей (т. е. ионов), то полная сила, действующая между всеми ионами в сечении, перед разрушением образца равна F = NFmax. Отсюда максимальное напряжение
где Fmax определяется формулой (1.5.1). Оценим эту величину. Диаметр иона приближенно равен расстоянию между ионами в равновесии, т. е. r0. Тогда число ионов (а значит, и связей) в сечении единичной площади приближенно равно:
Следовательно, теоретическое значение предела прочности кристалла NaCl равно:
Конечно, нельзя считать, что эта оценка получена чисто теоретически, исходя из определенных представлений о строении вещества. Мы ведь заимствовали из эксперимента значение εmax перед разрушением (см. рис. 1.8, на котором схематически изображен разрыв кристалла). Оценка модуля ЮнгаЧтобы оценить модуль Юнга, нужно сделать еще одно довольно грубое допущение. Будем считать, что закон Гука выполняется при любых деформациях, вплоть до разрыва. Тогда σпч = Еεmax, где Е — модуль Юнга. Отсюда
|
|
|



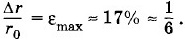 При этой деформации смещение ионов от положения равновесия Δr = εmaxr0. Расстояние между ионами в момент достижения максимальной деформации равно: г = r0 + Δr = r0(1+ εmax)(РИС. 1.8).
При этой деформации смещение ионов от положения равновесия Δr = εmaxr0. Расстояние между ионами в момент достижения максимальной деформации равно: г = r0 + Δr = r0(1+ εmax)(РИС. 1.8).