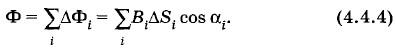|
|
|
|
|
Глава 4. Магнитное поле токов § 4.4. Поток магнитной индукцииМагнитный потокВектор магнитной индукции
Выделим в магнитном поле настолько малый элемент поверхности площадью ΔS, чтобы магнитную индукцию во всех его точках можно было считать одинаковой. Пусть ΔФ = BΔS cos α. (4.4.1) Произведение В cos α = Вn представляет собой проекцию вектора магнитной индукции на нормаль к элементу. Поэтому
Поток может быть как положительным, так и отрицательным в зависимости от значения угла α. Если магнитное поле однородно, то поток через плоскую поверхность площадью S равен: Ф = BS cos α. (4.4.3) Поток магнитной индукции наглядно может быть истолкован как величина, пропорциональная числу линий вектора * Точнее, как разность числа линий вектора магнитной индукции
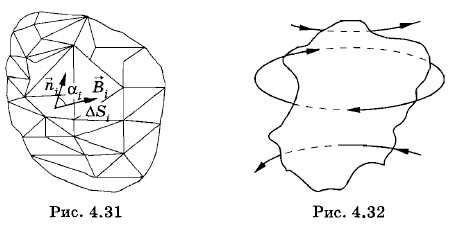
Поток магнитной индукции через поверхность произвольного размера и формы определяют следующим образом. Всю поверхность разбивают на столь малые элементарные площадки ΔSi, чтобы магнитную индукцию на каждой из площадок
можно было считать одинаковой во всех точках (рис. 4.31); строят к каждой площадке нормаль ΔФi = BiΔSi cos αi. Суммируя элементарные потоки ΔФi, находят полный поток через поверхность:
Поверхность может быть замкнутой*. * Если поверхность замкнута, то положительной нормалью к поверхности принято считать внешнюю нормаль. В этом случае число линий индукции, входящих внутрь поверхности, равно числу линий, выходящих из нее (рис. 4.32).
|
|
|



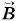 характеризует магнитное поле в каждой точке пространства. Введем еще одну величину, зависящую от значения вектора магнитной индукции не в одной точке, а во всех точках произвольно выбранной поверхности. Эту величину называют потоком вектора магнитной индукции, или магнитным потоком. Она аналогична понятию потока вектора электрической напряженности.
характеризует магнитное поле в каждой точке пространства. Введем еще одну величину, зависящую от значения вектора магнитной индукции не в одной точке, а во всех точках произвольно выбранной поверхности. Эту величину называют потоком вектора магнитной индукции, или магнитным потоком. Она аналогична понятию потока вектора электрической напряженности.
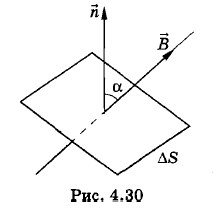
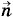 — нормаль к элементу, образующая угол α с направлением вектора магнитной индукции (рис. 4.30). Потоком вектора магнитной индукции через поверхность площадью ΔS называют величину, равную произведению модуля вектора магнитной индукции
— нормаль к элементу, образующая угол α с направлением вектора магнитной индукции (рис. 4.30). Потоком вектора магнитной индукции через поверхность площадью ΔS называют величину, равную произведению модуля вектора магнитной индукции