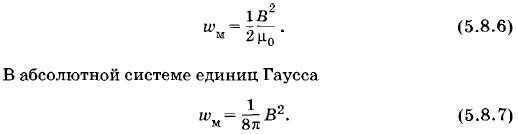|
|
|
|
|
Глава 5. Электромагнитная индукция § 5.8. Энергия магнитного поля тока
Энергия тока, о которой сейчас пойдет речь, совсем иной природы, чем энергия, выделяемая постоянным током в цепи в виде теплоты, количество которой определяется законом Джоуля—Ленца. При замыкании цепи, содержащей источник постоянной ЭДС, энергия источника тока первоначально расходуется на создание тока, т. е. на приведение в движение электронов проводника и образование связанного с током магнитного поля, а также отчасти на увеличение внутренней энергии проводника, т. е. на его нагревание. После того как установится постоянное значение силы тока, энергия источника расходуется исключительно на выделение теплоты. Энергия тока при этом уже не изменяется. Точно так же, для того чтобы разогнать автомашину на горизонтальном участке пути до постоянной скорости υ, нужно совершить работу Выясним теперь, почему же для создания тока необходимо затратить энергию, т. е. необходимо совершить работу. Объясняется это тем, что при замыкании цепи, когда ток начинает нарастать, в проводнике появляется вихревое электрическое поле, действующее против того электрического поля*, которое создается в проводнике благодаря источнику тока. Для того чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля. Эта работа и идет на увеличение энергии тока. Вихревое поле совершает отрицательную работу. * Это электрическое поле создается заряженными частицами на поверхности проводника в отличие от вихревого поля, порождаемого переменным магнитным полем. При размыкании цепи ток исчезает и вихревое поле совершает положительную работу. Запасенная током энергия выделяется. Это обнаруживается по мощной искре, возникающей при размыкании цепи с большой индуктивностью. Записать выражение для энергии тока I, текущего по цепи с индуктивностью L, можно на основании аналогии между инерцией и самоиндукцией, о которой говорилось в § 5.7. Если самоиндукция аналогична инерции, то индуктивность в процессе создания тока должна играть ту же роль, что и масса при увеличении скорости тела в механике. Роль скорости тела в электродинамике играет сила тока I как величина, характеризующая движение электрических зарядов. Если это так, то энергию тока WM можно считать величиной, подобной кинетической энергии тела
Именно такое выражение для энергии тока и получается в результате расчетов. Работа А, совершаемая источником с ЭДС А = Согласно закону сохранения энергии эта работа равна сумме приращения энергии тока ΔWM и количества выделяемой теплоты Q = I2RΔt: A = ΔWM + Q. (5.8.2) Отсюда приращение энергии тока ΔWM = A - Q = IΔt( Согласно закону Ома для полной цепи IR = где
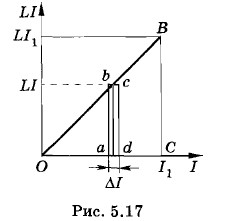
На графике зависимости LI от I (рис. 5.17) приращение энергии численно равно площади прямоугольника abed со сторонами ΔWM. Полное изменение энергии при возрастании тока от нуля до I1 численно равно площади треугольника ОВС со сторонами I1 и LI1. Следовательно,
Энергия тока, определяемая формулой (5.8.1), выражена через характеристику проводника L и силу тока в нем I. Но эту же энергию можно выразить и через характеристики поля. Вычисления показывают, что плотность энергии магнитного поля
|
|
|



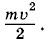 Часть мощности двигателя при этом тратится на преодоление трения, а часть — на увеличение скорости машины. При υ = const вся мощность двигателя расходуется на преодоление трения, а кинетическая энергия машины не меняется.
Часть мощности двигателя при этом тратится на преодоление трения, а часть — на увеличение скорости машины. При υ = const вся мощность двигателя расходуется на преодоление трения, а кинетическая энергия машины не меняется.
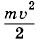 в механике, и записать в виде:
в механике, и записать в виде:

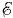 за малое время Δt, равна:
за малое время Δt, равна:
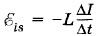 — ЭДС самоиндукции. Заменяя в уравнении (5.8.3) произведение IR его значением (5.8.4), получим:
— ЭДС самоиндукции. Заменяя в уравнении (5.8.3) произведение IR его значением (5.8.4), получим:
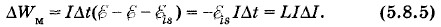
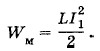
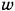 м (т. е. энергия единицы объема) пропорциональна квадрату магнитной индукции, подобно тому как плотность энергии электрического поля пропорциональна квадрату напряженности электрического поля. В вакууме в единицах СИ
м (т. е. энергия единицы объема) пропорциональна квадрату магнитной индукции, подобно тому как плотность энергии электрического поля пропорциональна квадрату напряженности электрического поля. В вакууме в единицах СИ