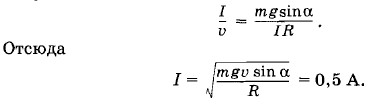|
|
|
|
|
Глава 5. Электромагнитная индукция § 5.9. Примеры решения задачПри решении задач на материал этой главы нужно уметь с помощью правила Ленца определять направление индукционного тока. Для вычисления ЭДС индукции следует использовать формулы (5.3.3), (5.5.2), а для ЭДС самоиндукции и взаимной индукции — формулы (5.7.2) и (5.7.4). Энергию тока вычисляют по формуле (5.8.1), а плотность энергии магнитного поля — по формуле (5.8.6). Для решения некоторых задач надо применять закон Ампера (4.7.9). Задача 1Проволочное кольцо радиусом r находится в однородном магнитном поле, индукция которого перпендикулярна плоскости кольца и меняется с течением времени по закону В = kt. Определите напряженность электрического поля в витке. Решение. Согласно закону электромагнитной индукции (5.3.2)
С другой стороны, ЭДС индукции численно равна работе, совершаемой вихревым электрическим полем при перемещении единичного положительного заряда вдоль проволочного кольца (см. § 4.4), т. е. | Сравнивая выражения (5.9.1) и (5.9.2), получим: 2πrE = kπr2. Отсюда
Задача 2
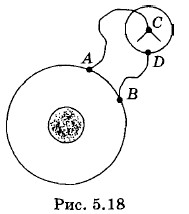
В однородном проволочном кольце создан постоянный индукционный ток I. Линии индукции переменного магнитного поля, создающего этот ток, перпендикулярны плоскости кольца. Поле сосредоточено вблизи его оси и имеет ось симметрии, проходящую через центр кольца (рис. 5.18). Чему равна разность потенциалов между точками А и В? Что будет показывать электрометр, присоединенный к этим точкам? Решение. Разность потенциалов между любыми точками кольца должна быть равна нулю. В противном случае мы придем к противоречию, применяя закон Ома к короткому и длинному участкам кольца. Кроме того, это очевидно и из соображений симметрии. Отсутствие разности потенциалов означает, что кулоновское поле внутри кольца равно нулю. Ток возникает вследствие наличия ЭДС индукции, распределенной равномерно вдоль кольца:
где еi, и Несмотря на отсутствие разности потенциалов между точками A и В, электрометр обнаружит разность потенциалов между стержнем и корпусом. Дело в том, что в проводниках АС и BD ток равен нулю. Следовательно, в каждой точке этих проводников стороннее электрическое поле индукционного происхождения уравновешивается кулоновским (потенциальным) полем, возникающим вследствие перераспределения зарядов в проводниках под влиянием ЭДС индукции. Работа потенциальных сил при перемещении по замкнутому контуру ACDBA равна нулю. На участке АВ кулоновское поле отсутствует. При перемещении единичного заряда по проводникам АС и BD работа потенциальных сил численно равна ЭДС индукции в этих проводниках и имеет противоположный знак. Следовательно, для равенства нулю работы кулоновских сил вдоль замкнутого контура необходимо, чтобы разность потенциалов между точками С и D равнялась ЭДС индукции в проводниках АС и DB и совпадала с ней по знаку. Так как ЭДС индукции в замкнутом контуре ACDBA равна нулю (магнитное поле не пронизывает этот контур), то на участке АВ ЭДС индукции равна по модулю и противоположна по знаку ЭДС в проводниках АС и ВП, если пренебречь работой сторонних сил индукции на участке между стержнем и корпусом электрометра по сравнению с работой в проводниках АС и BD. Поэтому электрометр покажет разность потенциалов, приблизительно равную ЭДС на участке АВ. Задача 3По параллельным рельсам, наклоненным под углом α = 30° к горизонту, соскальзывает без трения с постоянной скоростью υ = 1м/с проводящая перемычка массой m = 100 г. В своей верхней части рельсы замкнуты проводником. Рельсы с перемычкой находятся в однородном магнитном поле, индукция которого направлена вертикально. Сопротивление перемычки R = 2 Ом гораздо больше сопротивления остальной части системы. Чему равна сила тока I в перемычке?
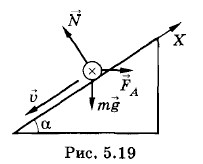
Решение. На перемычку действуют три силы: сила тяжести Так как, согласно условию, перемычка соскальзывает по рельсам с постоянной скоростью без трения, то векторная сумма действующих на нее сил равна нулю:
Запишем это уравнение для модулей проекций на ось X, направленную так, как показано на рисунке 5.19: FA cos α = mg sin α. (5.9.3) Сила Ампера, действующая со стороны магнитного поля на перемычку, равна: FA = BIl, где В — индукция магнитного поля, l — длина перемычки. Тогда уравнение (5.9.3) примет вид: BIl cos α = mg sin α. (5.9.4) ЭДС индукции, возникающая в перемычке при ее движении вниз по рельсам со скоростью
Согласно закону Ома Blυ cos α = IR. (5.9.5) Поделив почленно равенство (5.9.4) на равенство (5.9.5), получим:
|
|
|



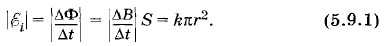
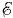 i| = 2πrE. (5.9.2)
i| = 2πrE. (5.9.2)
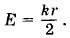
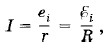
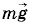 , сила реакции рельсов
, сила реакции рельсов 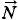 и сила Ампера
и сила Ампера 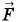 А, направленная вправо (рис. 5.19). Направление силы Ампера не зависит от направления вектора
А, направленная вправо (рис. 5.19). Направление силы Ампера не зависит от направления вектора 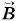 . При изменении направления
. При изменении направления 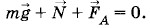
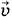 , равна:
, равна: