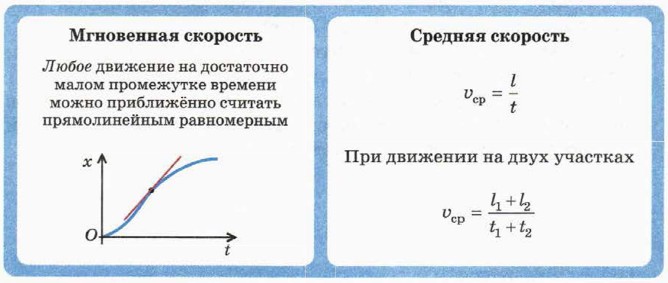
Дополнительные вопросы и задания к § 4: Мгновенная и средняя скорость

Что мы узнали из § 4

Дополнительные вопросы и задания § 4

12. Одну треть всего времени движения поезд ехал со скоростью υ₁, а оставшееся время — со скоростью υ₂.

а) Выразите пройденный поездом путь через υ₁, υ₂ и всё время движения t.

б) Выразите среднюю скорость поезда через υ₁ и υ₂.

в) Найдите числовое значение средней скорости при υ₁ = 60 км/ч, υ₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью υ₁ а оставшийся участок пути — со скоростью υ₂.

а) Выразите всё время движения автомобиля через υ₁, υ₂ и весь пройденный путь l.

б) Выразите среднюю скорость движения автомобиля через υ₁ и υ₂.

в) Найдите числовое значение средней скорости при υ₁ = 80 км/ч, υ₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всём пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображённый на рисунке 4.4. Считайте, что автомобиль едет вдоль оси х.

а) Определите графически среднюю скорость за 6 с.

б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси х. Зависимость координаты тела от времени выражается формулой х = 0,2 • t².

а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.

б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за всё время движения.

<<< К началу Ответы и указания >>>