|
|
|
|
|
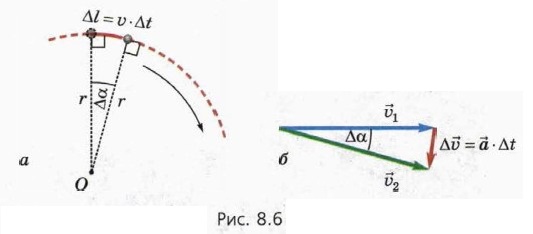
§ 8. Равномерное движение по окружности Ускорение при равномерном движении по окружности (окончание)Модуль ускоренияЗа промежуток времени Δt тело, движущееся со скоростью υ, проходит по дуге окружности путь Δl = υ • Δt (это красная сплошная линия на рисунке 8.6, а).
Если Δt мало по сравнению с Т, эта дуга почти не отличается от отрезка прямой. Поэтому фигура, образованная двумя радиусами r и этим отрезком, представляет собой равнобедренный треугольник с основанием Δl = υ • Δt. Этот треугольник подобен равнобедренному треугольнику, образованному скоростями
откуда получаем:
Центростремительное ускорение можно выразить также через ν и r или через Т и r.
Подсказка. Воспользуйтесь формулами (4), (1), (2). Можно подумать, что центростремительное ускорение, обусловленное изменением только направления скорости, не может быть значительным. Убедимся, что это не всегда так.
а) С каким ускорением движется космонавт, когда центрифуга делает шесть оборотов в минуту? б) При какой частоте обращения космонавт движется с ускорением, превышающим ускорение свободного падения в 10 раз? Чему равна при этом его линейная скорость? Чтобы испытать на себе ощущения при движении с ускорением, в несколько раз превышающем ускорение свободного падения, можно покататься на центрифуге в парке (рис. 8.8). 9
|
|
|



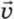 1,
1, 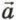 • Δt (он изображён на рисунке 8.6, б), поскольку углы при вершинах этих треугольников равны. Следовательно, основания указанных двух треугольников относятся, как их боковые стороны:
• Δt (он изображён на рисунке 8.6, б), поскольку углы при вершинах этих треугольников равны. Следовательно, основания указанных двух треугольников относятся, как их боковые стороны:
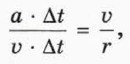

 7. Докажите, что центростремительное ускорение выражается также формулами
7. Докажите, что центростремительное ускорение выражается также формулами


