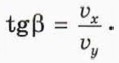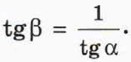|
|
|
|
|
|
§ 12. Относительное движение брошенных тел. Отскок от наклонной плоскости Отскок мяча от наклонной плоскости (окончание)
Найдём соотношение между углом наклона плоскости α и углом β отражения мяча после второго удара (рис. 12.3). Для этого надо найти проекции скорости мяча сразу после второго удара о плоскость.
υx = 3υ0 sin α, υy = υ0 cos α. П о д с к а з к а. Воспользуйтесь тем, что в результате удара о плоскость проекция скорости мяча на ось х не изменяется, а проекция скорости на ось у изменяет знак, а также формулами зависимости проекций скорости мяча от времени и выражением для промежутка времени τ между двумя ударами.
tgβ = 3tgα. П о д с к а з к а. Воспользуйтесь тем, что сразу после второго удара
П о д с к а з к а. Воспользуйтесь тем, что в таком случае α + β = 90°, поэтому
|
|
|



 8. Выразите расстояние d между точками первых двух ударов мяча о плоскость через
8. Выразите расстояние d между точками первых двух ударов мяча о плоскость через 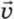 0, α и g.
0, α и g.