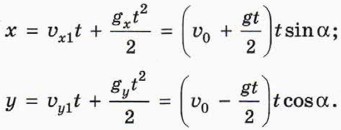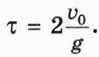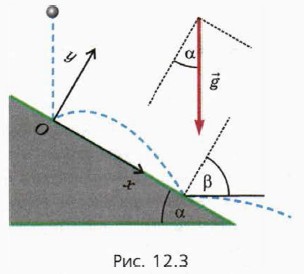
Отскок мяча от наклонной плоскости

Мяч свободно падает без начальной скорости с высоты h на наклонную плоскость с углом наклона а, отскакивает от неё и затем снова ударяется о плоскость (рис. 12.3).

рис. 12.3

Будем считать, что в результате столкновения мяча с плоскостью модуль скорости мяча не изменяется, а угол отражения равен углу падения¹.

¹ Углы падения и отражения — это углы между скоростью мяча и перпендикуляром к наклонной плоскости непосредственно перед ударом мяча о плоскость и после удара.

Выясним:

1) чему равен промежуток времени τ между ударами?

2) чему равно расстояние d между точками ударов?

Обычно при рассмотрении ситуаций, в которых речь идёт о наклонной плоскости, удобно направить ось х вдоль наклонной плоскости вниз, а ось у — перпендикулярно наклонной плоскости вверх (см. рис. 12.3).

Обозначим ₀ скорость мяча непосредственно перед первым ударом о плоскость, a ₁ — скорость сразу после удара. Угол отражения мяча от наклонной плоскости после первого удара равен α, а угол отражения после второго удара мы обозначим β (мы его тоже найдём).

5. Объясните, почему зависимость проекций скорости мяча от времени между ударами задаётся уравнениями

υ_x = υ_x1 + g_xt = (υ₀ + gt) sin α,

υ_y = υ_y1 + g_yt = (υ₀ - gt) cos α.

6. Объясните, почему зависимость координат мяча от времени между ударами задаётся уравнениями

7. Получите формулу для промежутка времени τ между первым и вторым ударами мяча о плоскость:

П о д с к а з к а. Воспользуйтесь тем, что при ударе мяча о плоскость координата мяча у = 0.

Итак, промежуток времени между ударами не зависит от угла наклона плоскости α! Он определяется только модулем скорости в момент падения мяча, то есть начальной высотой h.

Окончание >>>