|
|
|
|
|
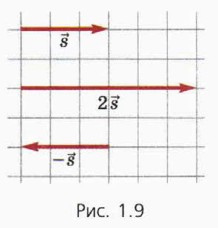
§ 1. Система отсчёта, траектория, путь и перемещение Действия с векторными величинамиВекторные величины1 широко используют в физике: это, например, перемещение, скорость, ускорение. Векторную величину обозначают буквой со стрелкой над ней, а модуль этой величины — той же буквой, но без стрелки. Например, перемещение обозначают 1 Часто для краткости их называют просто векторами. Напомним действия с векторами, уже знакомые вам из курса математики. Напомним действия с векторами, уже знакомые вам из курса математики. а) Умножение вектора на число При умножении вектора на число его модуль умножают на это число. Важно помнить: если это число отрицательно, то направление вектора изменяется на противоположное. На рисунке 1.9 изображены векторы
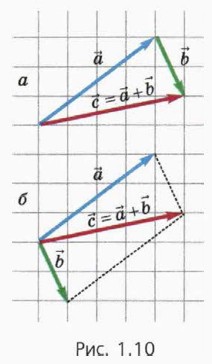
б) Сложение векторов Две векторные величины складывают по правилу треугольника (рис. 1.10, а) или по правилу параллелограмма (рис. 1.10, б). Результат сложения один и тот же, поэтому при выборе правила сложения исходят из соображений удобства.
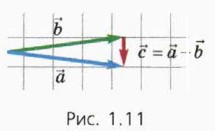
в) Вычитание векторов Чтобы вычесть из вектора
Мы намеренно выбрали случай, когда векторы
|
|
|



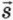 , а модуль перемещения — s.
, а модуль перемещения — s.
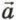 вектор
вектор 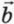 , можно отложить эти векторы из одной точки и соединить направленным отрезком конец вектора
, можно отложить эти векторы из одной точки и соединить направленным отрезком конец вектора 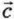 =
= 
 10. Вектор
10. Вектор