|
|
|
|
|
§ 1. Система отсчёта, траектория, путь и перемещение Действия с векторными величинами (окончание)Проекции векторных величинДействия с векторными величинами часто упрощаются, если использовать проекции1 этих величин на оси координат. Проекцию вектора обозначают той же буквой, что и сам вектор, но без стрелки и с индексом внизу, указывающим ось координат. Например, проекцию вектора 1 В школьном курсе геометрии проекции вектора называют координатами вектора. Чтобы найти проекцию вектора на ось координат, проецируют изображающий этот вектор отрезок на данную ось, а затем приписывают проекции знак « + » или «-» в зависимости от того, как направлен данный вектор относительно выбранной оси. На рисунке 1.12 показано, как находить проекции векторов на оси координат х и у.
Обратите внимание, что проекция вектора может быть положительной, отрицательной или равной нулю. При умножении вектора на число все проекции этого вектора умножаются на то же число. При сложении векторов их проекции складываются, а при вычитании — вычитаются. Например, если
а) вектор, у которого обе проекции на оси координат х, у отрицательны; б) два вектора с общим началом, модули которых не равны, а проекции на ось х равны; в) два вектора с общим началом, модули которых равны, а проекции на ось у не равны. <<< К началу Вопросы и задания >>>
|
|
|



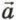 на ось х обозначают аx.
на ось х обозначают аx.
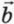 +
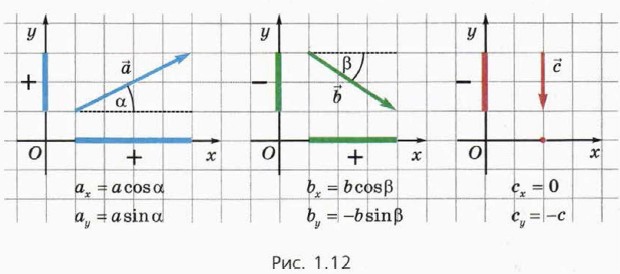
+ 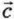 , то ах = bх + сх; ау = bу + су.
, то ах = bх + сх; ау = bу + су.
 11. Изобразите на чертеже в тетради:
11. Изобразите на чертеже в тетради: