|
|
|
|
|
§ 2. Прямолинейное равномерное движение График зависимости координаты от времениИз определения скорости (1) получаем соотношение между проекциями скорости и перемещения (например, на ось x):
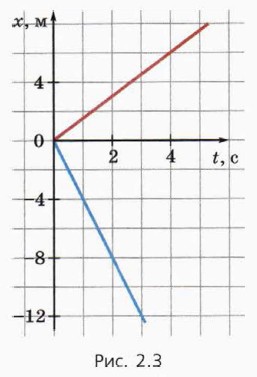
Направим ось х вдоль прямой, по которой движется тело, и совместим начало координат с начальным положением тела (оно отмечено светлым кружком на рисунке 2.2). Тогда
sx = х, (3) причём sx положительно, если тело переместилось в положительном направлении оси х (рис. 2.2, а), и отрицательно, если тело переместилось в отрицательном направлении оси х (рис. 2.2, б). Из формул (2) и (3) получаем в этом случае:
Проекция скорости υx > 0, когда тело движется в положительном направлении оси х (рис. 2.2, а); если тело движется в отрицательном направлении оси х, то υx < 0. Из формулы (4) следует, что зависимость координаты тела от времени выражается формулой х = υxt. (5) Итак, при прямолинейном равномерном движении из начала координат координата тела х прямо пропорциональна проекции скорости υx. График такой зависимости — отрезок прямой, один из концов которого совпадает с началом координат. Значение координаты х увеличивается со временем, если υx > 0, то есть когда тело движется в положительном направлении оси х, и уменьшается со временем, если υx < 0, то есть когда тело движется в отрицательном направлении оси х.
а) Каким цветом изображён график для пешехода? б) В каком направлении оси х ехал велосипедист? в) Чему равны модули скорости пешехода и велосипедиста? г) Перенесите графики в тетрадь и добавьте к ним график зависимости координаты от времени для автомобиля, который едет в отрицательном направлении оси х, если модуль его скорости в 5 раз больше модуля скорости велосипедиста.
|
|
|




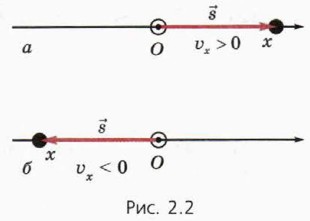

 4. На рисунке 2.3 изображены графики зависимости координаты от времени для пешехода и велосипедиста.
4. На рисунке 2.3 изображены графики зависимости координаты от времени для пешехода и велосипедиста.