|
|
|
|
|
|
§ 24. Движение системы тел. Учёт трения между телами системы Тела в начальном состоянии движутся друг относительно другаПусть на гладком столе лежит доска длиной L и массой mд. На краю доски находится не- большой брусок массой mб. (рис. 24.1). Коэффициент трения между бруском и доской μ. В начальный момент доска покоится, а бруску толчком сообщают начальную скорость
Как будут двигаться тела? При скольжении бруска по доске на него и на доску действуют противоположно направленные равные по модулю силы трения скольжения
Возможны два варианта дальнейшего развития событий: 1) брусок будет скользить по доске, пока их скорости не станут равными, то есть пока брусок не остановится относительно доски. Начиная с этого момента силы трения перестанут действовать на доску и брусок, и они будут скользить по гладкому столу вместе как единое целое с постоянной конечной скоростью
2) скорости бруска и доски не успеют сравняться до того момента, когда брусок дойдёт до противоположного конца доски. В таком случае брусок соскользнёт с доски, после чего они будут двигаться по столу с различными скоростями
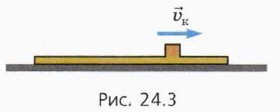
Рассмотрим сначала случай, когда доска с бруском будут двигаться как единое целое (см. рис. 24.3), и выведем условие, при котором этот случай реализуется.
Найдём теперь условие того, что брусок будет скользить по доске до тех пор, пока их скорости не сравняются. Так произойдёт, если путь l, пройденный бруском относительно доски, не превышает длины доски L. Путь l мы найдём, определив ускорение бруска относительно доски.
|
|
|



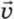 0, направленную вдоль доски.
0, направленную вдоль доски.
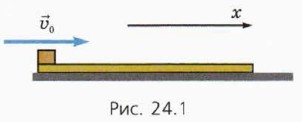
 тp1 и
тp1 и 
 1. Как зависят от времени проекции скорости бруска и доски на ось х, показанную на рисунке 24.1?
1. Как зависят от времени проекции скорости бруска и доски на ось х, показанную на рисунке 24.1?