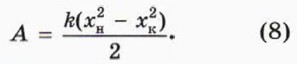|
|
|
|
|
|
§ 28. Механическая работа. Мощность Работа силы упругостиКогда пружина возвращается в недеформированное состояние, сила упругости
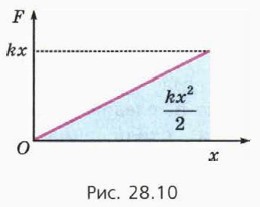
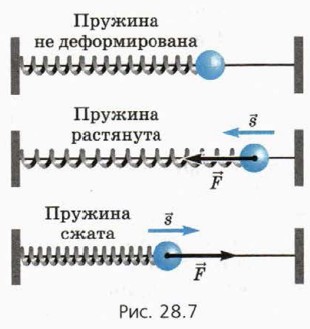
Найдём работу силы упругости Модуль этой силы связан с модулем деформации х соотношением (см. § 15) F = kx. (6) Работу такой силы можно найти графически. Заметим сначала, что работа постоянной силы численно равна площади прямоугольника под графиком зависимости силы от перемещения (рис. 28.8).
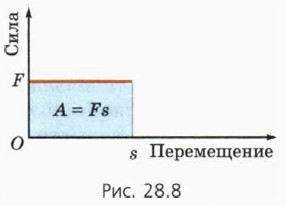
На рисунке 28.9 изображён график зависимости F(x) для силы упругости. Разобьём мысленно всё перемещение тела на столь малые промежутки, чтобы на каждом из них силу можно было считать постоянной.
Тогда работа на каждом из этих промежутков численно равна площади фигуры под соответствующим участком графика. Вся же работа равна сумме работ на этих участках. Следовательно, и в этом случае работа численно равна площади фигуры под графиком зависимости F(x).
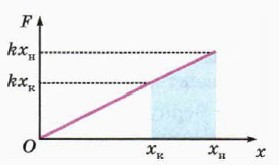
Из формулы (8) мы видим, что работа силы упругости зависит только от начальной и конечной деформации пружины. Поэтому если тело сначала деформируют, а потом оно возвращается в начальное состояние, то работа силы упругости равна нулю. Напомним, что таким же свойством обладает и работа силы тяжести.
а) Чему равна конечная деформация пружины? б) Чему равна работа силы упругости пружины?
|
|
|



 совершает всегда положительную работу: её направление совпадает с направлением перемещения
совершает всегда положительную работу: её направление совпадает с направлением перемещения 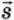 (рис. 28.7).
(рис. 28.7).
 7. Используя рисунок 28.10, докажите, что
7. Используя рисунок 28.10, докажите, что