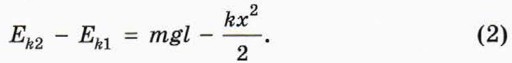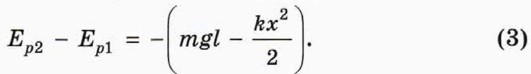Когда механическая энергия сохраняется

Из курса физики основной школы вы уже знаете, что

сумму кинетической и потенциальной энергий называют полной механической энергией.

Докажем, что

полная механическая энергия замкнутой системы тел, взаимодействующих посредством сил упругости и тяготения, сохраняется, то есть её изменение равно нулю:

Δ(Е_k + Е_р) = 0. (1)

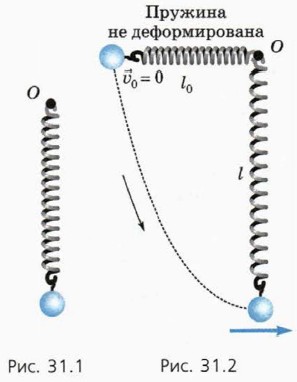
Это утверждение называют законом сохранения энергии в механике. Его доказательство мы получим как обобщение примера, рассмотрение которого поможет вам и при решении задач.

Возьмём шар массой m, подвешенный к лёгкой пружине, которая может вращаться вокруг горизонтальной оси О (рис. 31.1).

Отклоним шар так, чтобы пружина была горизонтальна и не деформирована (рис. 31.2), и отпустим его без толчка. Шар начнёт двигаться вниз по некоторой кривой, а пружина при этом будет растягиваться.

Рис. 31.1

Обозначим l длину пружины в тот момент, когда шар находится в нижней точке траектории. При этом удлинение пружины х = lm - l₀, где l₀ — длина недеформированной пружины. Чему равна при этом кинетическая энергия шара?

Ответ на этот вопрос мы найдём с помощью теоремы об изменении кинетической энергии, которая является следствием второго закона Ньютона. Согласно этой теореме изменение кинетической энергии шара равно алгебраической сумме работ всех приложенных к нему сил.

На шар действуют сила тяжести и сила упругости пружины. При движении от верхней точки до нижней шар переместился вниз на расстояние l, а деформация пружины стала равной х.

1. Чему равна работа силы тяжести при движении шара от верхней точки до нижней?

2. Чему равна при этом работа силы упругости?

3. Чему равна алгебраическая сумма работы силы тяжести и силы упругости?

Выполнив эти задания, вы увидите, что изменение кинетической энергии шара выражается формулой

Найдём теперь изменение потенциальной энергии системы «шар + пружина + Земля». По определению потенциальной энергии её изменение равно взятой со знаком минус суммарной работе сил упругости и тяготения (см. § 30). Выражение именно для этой работы и стоит в правой части формулы (2). Поэтому

Сравнивая уравнения (2) и (3), мы видим, что потенциальная энергия системы уменьшилась ровно настолько же, насколько увеличилась кинетическая энергия шара! Поэтому полная механическая энергия системы сохраняется:

E_k2 + Е_р2 = E_k1 + Е_р1. (4)

Окончание >>>