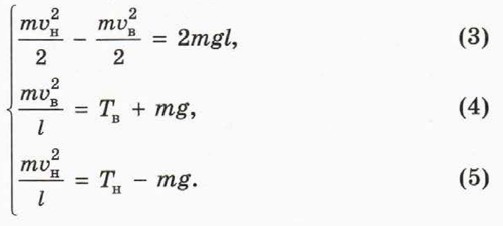Груз, подвешенный на нити и стержне (продолжение)

6. Объясните смысл следующих уравнений:

7. Подвешенный на нити шарик массой 100 г вращается в вертикальной плоскости. Насколько больше сила натяжения нити, когда шарик проходит положение равновесия, чем когда он находится в верхней точке окружности?

П о д с к а з к а. Удобно вычесть уравнение (4) из уравнения (5) и сравнить полученное уравнение с уравнением (3).

«Шестикратный вес»

Шарик движется по окружности при условии, что нить натянута. Поэтому минимальная скорость, которую нужно сообщить шарику в нижней точке, чтобы он стал двигаться по окружности, должна быть такой, чтобы сила натяжения нити обратилась в нуль только в верхней точке окружности.

8. Шарику, подвешенному на нити длиной l, сообщили в нижней точке минимальную горизонтальную скорость, необходимую для того, чтобы он начал двигаться по окружности. Сделайте чертёж, на котором изобразите силы, действующие на шарик в верхней и нижней точках окружности. Чему в этом случае равны:

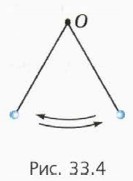
а) скорость шарика в верхней точке окружности?

б) ускорение шарика в верхней точке окружности?

в) скорость шарика в нижней точке окружности?

г) вес шарика в нижней точке окружности?

П о д с к а з к а. Воспользуйтесь уравнениями (3)—(5).

Итак, когда груз проходит нижнюю точку, нить должна выдерживать шестикратный вес груза!

В какой точке шарик сойдёт с окружности?

Пусть теперь скорость шарика в нижней точке недостаточна для того, чтобы он мог совершить полный оборот.

В таком случае есть две возможности.

1) Шарик не поднимется выше точки подвеса О. Тогда он начнёт колебаться между крайними положениями (рис. 33.4).

Рис. 33.4

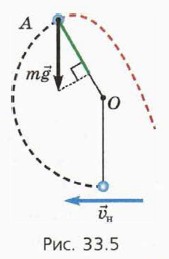
2) Шарик поднимется выше точки подвеса, но сила натяжения нити обратится в некоторой точке А в нуль (рис. 33.5). После этого шарик будет двигаться по параболе, показанной красным пунктиром. Когда шарик находится в точке А, центростремительное ускорение ему сообщает только составляющая силы тяжести, направленная вдоль радиуса к центру окружности. На рисунке показано, как найти модуль этой составляющей (отрезок зелёного цвета).

Рис. 33.5

<<< К началу Окончание >>>