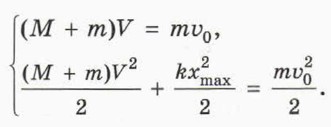|
|
|
|
|
|
§ 34. Движение системы тел Системы с пружинойПусть на гладком столе лежит груз массой М, к которому прикреплена пружина жёсткостью k (рис. 34.9). На эту систему налетает со скоростью
П о д с к а з к а. Для нахождения конечных скоростей груз и брусок можно рассматривать как тела, между которыми произошло упругое столкновение (см. § 32). Для ответа на этот вопрос не нужна жёсткость пружины. Деформация пружины максимальна в тот момент, когда брусок и груз сблизились на минимальное расстояние. При этом их скорости относительно стола равны. Обозначим xmax модуль деформации пружины, а V — общую скорость бруска и груза в этот момент.
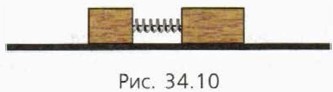
Рассмотрим теперь случай, когда надо учитывать трение. Пусть на столе покоятся небольшие бруски массой m1 и m2 (рис. 34.10). Между ними находится сжатая пружина жёсткостью k, которая удерживается нитью в деформированном состоянии. Модуль деформации пружины равен х. Коэффициент трения между брусками и столом равен μ. Когда нить пережгли, бруски разъехались на расстояние l друг от друга. Будем считать, что размерами брусков и пружины можно пренебречь по сравнению с l.
а) начальная механическая энергия системы? б) конечная механическая энергия этой системы? в) работа силы трения скольжения?
|
|
|



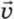 0 брусок массой m.
0 брусок массой m.
 16. Каковы проекции конечных скоростей груза и бруска на ось х, изображённую на рисунке 34.9?
16. Каковы проекции конечных скоростей груза и бруска на ось х, изображённую на рисунке 34.9?