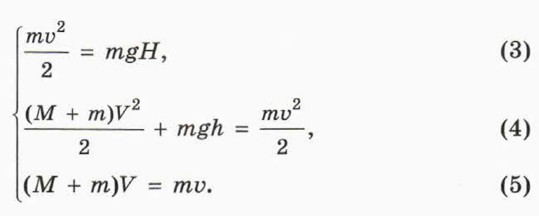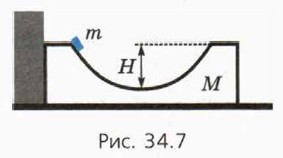
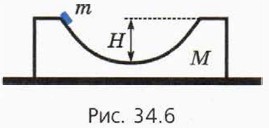
Гладкая горка и шайба (окончание)

Движение шайбы в бруске со сферической выемкой

Рассмотрим теперь случай, когда шайба движется во впадине между двумя вершинами гладкой горки. Такую «горку» представляют иногда как брусок с выемкой.

Пусть на гладком столе покоится брусок массой М с гладкой выемкой глубиной Н. На левый край выемки осторожно кладут шайбу массой m и без толчка отпускают (рис. 34.6).

Рис. 34.6

10. Какие физические величины сохраняются в данном случае?

11. Запишите систему уравнений, выражающую законы сохранения для момента, когда шайба проходит дно выемки.

12. Чему равно отношение массы шайбы к массе бруска, если максимальная скорость шайбы относительно стола равна 1,9 м/с, а глубина выемки равна 20 см?

Пусть теперь брусок находится у стены (рис. 34.7). Тогда движение тел удобно разделить на три этапа.

Рис. 34.7

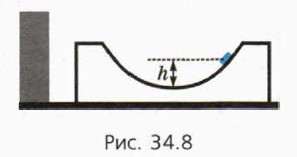
1. Спуск шайбы. При этом шайба давит на брусок силой, которая имеет горизонтальную составляющую, направленную влево. Но брусок не может двигаться влево, потому что упирается в стену. Стенка при этом давит на брусок, поэтому горизонтальная проекция суммарного импульса бруска и шайбы не сохраняется. Но сохраняется механическая энергия шайбы.

2. Подъём шайбы. Поднимаясь по правой стороне выемки, шайба давит на брусок силой, которая имеет горизонтальную составляющую, направленную вправо, поэтому он начнёт скользить по столу вправо. Теперь горизонтальная проекция суммарного импульса бруска и шайбы сохраняется. Их суммарная механическая энергия также сохраняется.

3. Момент, когда шайба поднялась на максимально возможную высоту h по правой стороне выемки (рис. 34.8). Достигнув высоты h, шайба на мгновенье останавливается относительно бруска, поэтому их скорости относительно стола будут равны и направлены горизонтально. Заметим, что h < Н, поскольку часть своей механической энергии шайба передала бруску.

Рис. 34.8

13. Шайба начала соскальзывать с высоты Н (см. рис. 34.7) и приобрела скорость и относительно стола, когда оказалась на дне выемки. Обозначим V общую скорость шайбы и бруска в момент, когда шайба поднялась на максимально возможную высоту h по правой стороне выемки. Объясните, почему справедливы следующие уравнения:

14. Выразите h через H, M, m.

П о д с к а з к а. Воспользуйтесь уравнением (5), чтобы выразить V через υ, М, m, и подставьте полученное выражение в (4). Получится система двух уравнений с двумя неизвестными (h и υ).

15. У стены на гладком столе покоится брусок массой 400 г с выемкой глубиной 15 см (см. рис. 34.7). На левый край выемки кладут шайбу и отпускают без толчка. Шайба поднимается по правой стороне выемки на высоту 10 см. Чему равна масса шайбы?

<<< К началу