|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела Движение с постоянным ускорениемДопустим, движение с постоянным ускорением совершается в одной плоскости, пусть это будет плоскость XOY. Если вектор начальной скорости и вектор ускорения не лежат на одной прямой, то точка будет двигаться по кривой линии. Следовательно, в этом случае с течением времени будут изменяться обе её координаты х и у. Обозначим через x0 и у0 координаты в начальный момент времени t0 = 0, а через х и у координаты в момент времени f. Тогда за время Δt = t — t0 = t изменения координат будут равны Δх = х - х0 и Δу = у - у0. Отсюда х = х0 + Δх, (1.13)
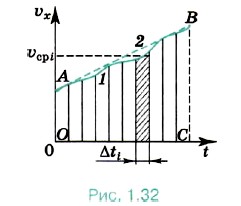
Значит, для нахождения положения точки в любой момент времени надо знать её начальные координаты и уметь находить изменения координат Δх и Δу за время движения. В случае движения, при котором проекция скорости изменяется со временем (рис. 1.32, кривая 1), величину Δx: за время t найдём следующим образом. Из § 4 мы знаем, что при равномерном движении изменение координаты точки за время Δt можно определить на графике зависимости
Разделим его на малые интервалы Δt, в пределах которых проекцию скорости можно считать постоянной и равной её среднему значению. Рассмотрим интервал Δti Тогда Δxi = В случае равноускоренного (ах = const) движения (рис. 1.32, прямая 2) изменение координаты тела Δх численно равно площади трапеции АВСО. Длины оснований ОА и ВС этой трапеции численно равны проекциям начальной и конечной скоростей, а длина высоты ОС — времени движения.
По формуле для площади трапеции имеем
Учитывая, что
Мы рассмотрели случай, когда Изменение координаты Δу можно найти таким же способом, и выражение имеет аналогичный вид
Подставив найденные выражения для изменения координат Δx и Δу в формулы (1.13), получим уравнения для координат при движении с постоянным ускорением как функции времени (их называют кинематическими уравнениями движения):
Обычно в условиях задачи даются значения (модули) скоростей и ускорений. Поэтому удобнее использовать уравнение
При движении точки в плоскости XOY двум уравнениям (1.14) соответствует одно векторное уравнение
Обратите внимание на то, что с помощью формул (1.14) и (1.15) можно найти только положение движущейся точки в любой момент времени. Для нахождения пути необходимо более подробно исследовать траекторию, определить точки, в которых, возможно, произошло изменение направления движения.
|
|
|



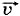 х(t) по площади прямоугольника. На рисунке 1.32 длина отрезка ОС численно равна времени движения.
х(t) по площади прямоугольника. На рисунке 1.32 длина отрезка ОС численно равна времени движения.
 Можно ли по графику зависимости
Можно ли по графику зависимости 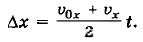
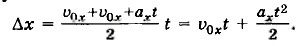
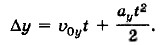
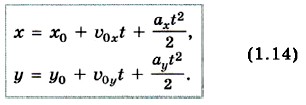
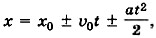 где υ0 и а — модули начальной скорости и ускорения. Очевидно, что в этом уравнении знак « + » берётся тогда, когда направления скорости
где υ0 и а — модули начальной скорости и ускорения. Очевидно, что в этом уравнении знак « + » берётся тогда, когда направления скорости 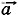 совпадают с направлением оси ОХ, знак «—» — когда они направлены в противоположную сторону.
совпадают с направлением оси ОХ, знак «—» — когда они направлены в противоположную сторону.
