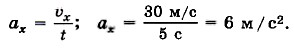|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 10. Движение с постоянным ускорениемКакая величина, характеризующая движение точки, не зависит от выбора системы отсчёта? Может ли в одной системе отсчёта точка покоиться, а в другой двигаться? Выясним зависимость скорости точки от времени при её движении с постоянным ускорением. Для этого воспользуемся формулой
Пусть
Если начальный момент времени t0 принять равным нулю, то получим
Отсюда получим формулу для определения скорости точки в любой момент времени при её движении с постоянным ускорением:
Векторному уравнению (1.11) соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси X и Y:
Как видим, при движении с постоянным ускорением скорость со временем меняется по линейному закону. Итак, для определения скорости в произвольный момент времени надо знать начальную скорость Ускорение же, наоборот, не зависит от того, что происходило с телом в предыдущие моменты, а зависит лишь от действия на него других тел в данный момент времени.
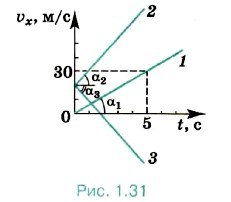
Зависимость проекции скорости от времени можно изобразить наглядно с помощью графика. Если начальная скорость равна нулю, то график зависимости проекции скорости на ось X от времени имеет вид прямой, выходящей из начала координат. Такая зависимость скорости от времени наблюдается при падении тела, покоившегося в начальный момент времени, с некоторой высоты или при движении автомобиля, трогающегося с места. На рисунке 1.31 представлен этот график в виде прямой 1 для случая ах > 0. По этому графику можно найти проекцию ускорения на ось X:
Чем больше ах, тем больший угол α с осью времени составляет график проекции скорости, так как за тот же промежуток времени скорость изменяется больше. Если начальная скорость отлична от нуля и тело движется с большим, но также постоянным ускорением, то график зависимости проекции скорости от времени имеет вид прямой 2 (см. рис. 1.31). В случае равнозамедленного движения с той же начальной скоростью график зависимости Теперь получим уравнения, которые позволяют рассчитывать для этого движения положение точки в любой момент времени.
|
|
|



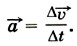
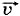 0 — скорость точки в начальный момент времени t0, а
0 — скорость точки в начальный момент времени t0, а 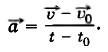
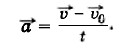
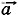 t. (1.11)
t. (1.11)
 Одинакова ли будет конечная скорость камня, если его сначала бросить вверх с некоторой начальной скоростью, а затем вниз с такой же начальной скоростью?
Одинакова ли будет конечная скорость камня, если его сначала бросить вверх с некоторой начальной скоростью, а затем вниз с такой же начальной скоростью?