|
|
|
|
|
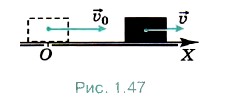
Глава 1. Кинематика точки и твёрдого тела § 12. Примеры решения задач по теме: Движение с постоянным ускорением.Для решения задач по этой теме необходимо правильно записывать уравнение движения и уравнение зависимости скорости от времени. Для некоторых задач разумно строить графики зависимости проекции скорости от времени и определять перемещение по графику, что часто удобнее, чем решать задачу аналитически. Задача 1. Ударом клюшки хоккейной шайбе сообщили скорость υ0 = 20 м/с. Через время t = 2 с скорость шайбы, движущейся прямолинейно, стала равна 16 м/с. Определите ускорение шайбы, считая его постоянным. Р е ш е н и е. Выберем оси координат так, чтобы движение шайбы происходило вдоль какой-нибудь координатной оси, например вдоль оси ОХ. За положительное направление оси ОХ примем направление вектора начальной скорости (рис. 1.47). Из определения ускорения следует: ах = (υ - υ0)/t = -2 м/с2.
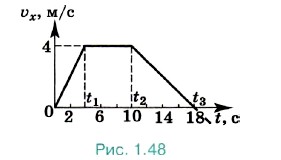
Знак «—» в конечном результате означает, что вектор ускорения направлен в сторону, противоположную положительному направлению оси ОХ. Модуль же ускорения а = |аx| = |-2 м/с2| = 2 м/с2. Задача 2. Перекрытие между первым и вторым этажами здания лифт проходил со скоростью υ0 = 4 м/с. Далее он начал тормозить и поднимался с постоянным ускорением а = 2 м/с2. Через время t = 2 с после начала торможения лифт остановился. Высота h каждого этажа равна 4 м. На какой высоте Н, считая от пола первого этажа, остановился лифт? Р е ш е н и е. Совместим начало координат с полом первого этажа и направим ось OY вертикально вверх. Так как ускорение лифта постоянно, то его движение будет описываться кинематическим уравнением у = у0 + υ0yt + ayt2/2. Согласно условию задачи у0 = h, υ0y = υ0, ау = -а, у = Н. Поэтому Н = h + υ0t - at2/2; Н = 8м. Задача 3. На рисунке 1.48 изображена зависимость проекции скорости от времени.
1) Постройте графики зависимости ускорения и перемещения от времени. 2) Определите перемещение за время, равное t3. 3) Определите среднюю скорость движения за время, равное t3.
|
|
|