|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела Примеры решения задач по теме: Второй закон НьютонаСогласно второму закону Ньютона m
При сделанном выборе направления оси X и начала координат имеем х0 = 0 и υ0x = -υ0. Проекцию ускорения ах на ось X найдём по второму закону Ньютона. Для рассматриваемого случая mах = mgx + Nx. Учитывая, что gx = g sinα и Nx = 0, получим ах = g sinα. Таким образом,
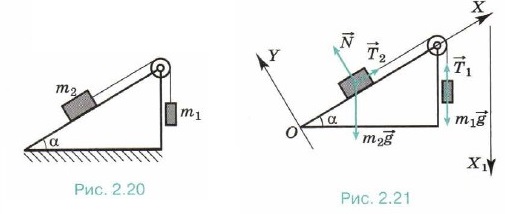
Задача 3. Два тела массами m1 = 10 г и m2 = 15 г связаны нерастяжимой и невесомой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (рис. 2.20). Плоскость образует с горизонтом угол α = 30°. Определите ускорение, с которым будут двигаться эти тела. Трение не учитывайте.
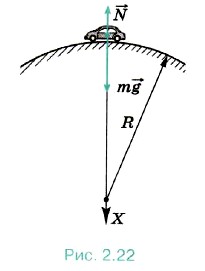
Р е ш е н и е. Предположим, что тело массой m1 перетягивает. Выберем оси координат так, как показано на рисунке 2.21. В проекциях на оси Х1 и X уравнения движения тел запишем в виде m1ax1 = m1g - Т1, m2ах = Т2 — m2g sinα, |ах| =|ax1|, так как нить нерастяжима. Силы натяжения нити равны, так как нить и блок невесомы. Сложив левые и правые части уравнении, получим Задача 4. Автомобиль массой т = 1000 кг движется со скоростью v = 36 км/ч по выпуклому мосту, имеющему радиус кривизны R = 50 м. С какой силой F давит автомобиль на мост в его середине? С какой минимальной скоростью umin должен двигаться автомобиль для того, чтобы в верхней точке он перестал оказывать давление на мост? Р е ш е н и е. Силы, действующие на автомобиль вдоль радиуса моста, изображены на рисунке 2.22: m
Отсюда F = N = m(g - υ2/R) = 7,8 кН. Сила давления на мост станет равной нулю при mυ2min/R = mg, так что υmin = 80 км/ч. При скорости, превышающей υmin, автомобиль оторвётся от поверхности моста.
|
|
|



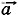 = m
= m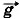 +
+ 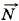 . Так как на брусок действуют постоянные силы, то вдоль оси X он будет двигаться с постоянным ускорением. Следовательно, чтобы определить положение бруска относительно точки О, можно воспользоваться кинематическим уравнением
. Так как на брусок действуют постоянные силы, то вдоль оси X он будет двигаться с постоянным ускорением. Следовательно, чтобы определить положение бруска относительно точки О, можно воспользоваться кинематическим уравнением
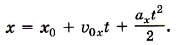
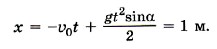
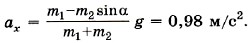 Так как ах > 0, то движение тел происходит в выбранном направлении.
Так как ах > 0, то движение тел происходит в выбранном направлении.
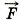 равна по модулю силе реакции моста
равна по модулю силе реакции моста