|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 23. Примеры решения задач по теме: Второй закон НьютонаПознакомимся с задачами, для решения которых не нужно знать, как зависят силы от расстояний между взаимодействующими телами (или частями одного тела) и от их скоростей. Единственное, что нам потребуется, — это выражение для силы тяжести вблизи поверхности Земли: Задача 1. К центру однородного шарика массой m = 0,2 кг приложена сила F = 1,5 Н. Определите модуль и направление силы
Р е ш е н и е. На шарик действуют две силы: сила Таким образом, искомая сила может быть направлена либо так же, как сила Проанализируем последнее выражение. Если mа > F, то F1x > 0, т. е. сила F1x - 0,2 • 5Н - 1,5 Н = -0,5 Н. Следовательно, сила F1 направлена противоположно оси X (рис. 2.18).
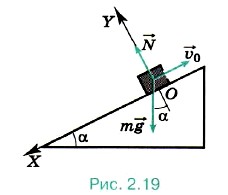
Задача 2. В результате полученного толчка брусок начал скользить вверх по наклонной плоскости из точки О с начальной скоростью υ0 = 4,4 м/с. Определите положение бруска относительно точки О через промежуток времени t1 — 2 с после начала его движения, если угол наклона плоскости к горизонту α = 30°. Трение не учитывайте. Р е ш е н и е. Поскольку требуется найти положение бруска относительно точки О, начало координат возьмём в этой точке. Ось X направим вдоль наклонной плоскости вниз, а ось Y — перпендикулярно этой плоскости вверх (рис. 2.19). При движении бруска на него действуют две силы: сила тяжести m
|
|
|



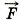 τ = m
τ = m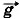 .
.
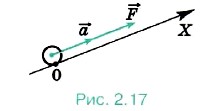
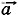 =
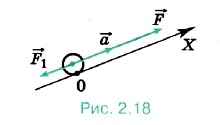
= 
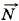 наклонной плоскости, перпендикулярная последней. Эту силу иногда называют силой нормальной реакции. Она всегда перпендикулярна поверхности, на которой находится тело.
наклонной плоскости, перпендикулярная последней. Эту силу иногда называют силой нормальной реакции. Она всегда перпендикулярна поверхности, на которой находится тело.