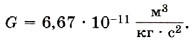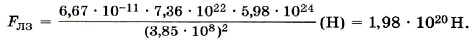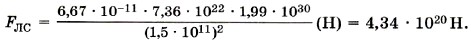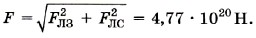|
|
|
|
|
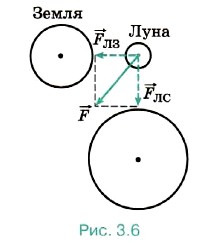
Глава 3. Силы в механике § 30. Примеры решения задач по теме: Закон всемирного тяготенияПри решении задач надо помнить, что сила тяготения действует между любыми телами, имеющими массу, но формула Задача 1. При опытной проверке закона всемирного тяготения сила взаимодействия между двумя свинцовыми шарами массами m1 = 5 кг и m2 = 500 г, расстояние между центрами которых r = 7 см, оказалась равной F = 34 нН. Вычислите по этим данным гравитационную постоянную. Р е ш е н и е. Согласно закону всемирного тяготения Получим Задача 2. Определите равнодействующую силу, действующую на Луну, считая, что силы притяжения к Земле и Солнцу взаимно перпендикулярны. Массы Луны, Земли и Солнца соответственно равны mЛ = 7,36 • 1022 кг; m3 = 5,98 • 1024 кг; mC = 1,99 • 1030 кг; расстояния от Луны до Земли и от Луны до Солнца соответственно равны rЛЗ = 3,85 • 108 м, rЛС = 1,5 • 1011 м. Р е ш е н и е. По условию задачи силы гравитационного притяжения Луны к Земле и Солнцу взаимно перпендикулярны (рис. 3.6). Рассчитаем силу гравитационного притяжения Луны к Земле.
Сила притяжения Луны к Солнцу равна
По теореме Пифагора найдём равнодействующую силу, действующую на Луну,
|
|
|



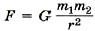 справедлива только для тел, которые можно считать материальными точками, а также для однородных тел шаровой формы. При этом расстояние r — это расстояние между центрами шаров.
справедлива только для тел, которые можно считать материальными точками, а также для однородных тел шаровой формы. При этом расстояние r — это расстояние между центрами шаров.
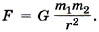 Из этого выражения следует, что
Из этого выражения следует, что 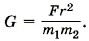 Подставим в эту формулу результаты опыта, при этом все данные переведём в СИ: m2 = 500 г = 5 • 10-1 кг, r = 7 см = 7 • 10-2 м, F = 34 нН = 3,4 • 10-8 Н.
Подставим в эту формулу результаты опыта, при этом все данные переведём в СИ: m2 = 500 г = 5 • 10-1 кг, r = 7 см = 7 • 10-2 м, F = 34 нН = 3,4 • 10-8 Н.
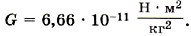 Уточнённое значение гравитационной постоянной, которое входит в таблицы:
Уточнённое значение гравитационной постоянной, которое входит в таблицы: