|
|
|
|
|
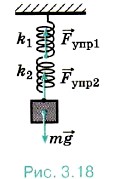
Глава 3. Силы в механике Примеры решения задач по теме: Силы упругости. Закон ГукаЗадача 3. К потолку подвешены последовательно две невесомые пружины жёсткостями 60 Н/м и 40 Н/м. К нижнему концу второй пружины прикреплён груз массой 0,1 кг. Определите жёсткость воображаемой пружины, удлинение которой было бы таким же, как и двух пружин при подвешивании к ней такого же груза (эффективную жёсткость). Р е ш е н и е. Так как весом пружин можно пренебречь, то очевидно, что силы натяжения пружин равны (рис. 3.18). Тогда согласно закону Гука Fynp1 = Fупр2; k1x1 = k2х2. (1)
На подвешенный груз действуют две силы — сила тяжести и сила натяжения второй пружины. Условие равновесия груза запишем в виде mg = k2х2. Из этого уравнения найдём удлинение Подставив выражение для х2 в уравнение (1), получим для удлинения Определим теперь эффективную жёсткость. Запишем закон Гука для воображаемой пружины:
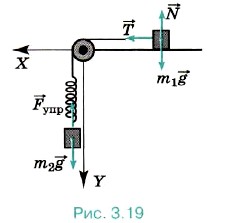
Подставив в формулу (2) выражения для удлинений x1 и х2 пружин, получим Для эффективной жёсткости получим выражение Задача 4. Через блок, закреплённый у края стола, перекинута нерастяжимая нить, к концам которой привязаны брусок массой m1 = 1 кг, находящийся на горизонтальной поверхности стола, и пружина жёсткостью k = 50 Н/м, расположенная вертикально. Ко второму концу пружины привязана гиря массой m2 = 200 г (рис. 3.19). Определите удлинение пружины при движении тел. Силу трения, массы пружины, блока и нити не учитывайте.
Р е ш е н и е. На брусок действуют сила тяжести, сила реакции опоры и сила натяжения нити. На гирю действуют сила тяжести и сила натяжения пружины. Согласно второму закону Ньютона для бруска и гири запишем: m1
|
|
|



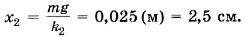
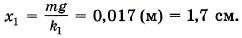
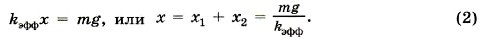
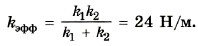
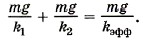
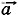 1 = m1
1 = m1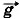 +
+ 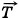 +
+ 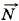 ;
;
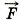 упр.
упр.