|
|
|
|
|
Глава 3. Силы в механике § 35. Примеры решения задач по теме: Силы упругости. Закон ГукаПри решении задач по этой теме надо иметь в виду, что закон Гука справедлив только при упругих деформациях тел. Сила упругости не зависит от того, какая происходит деформация: сжатия или растяжения, она одинакова при одинаковых Δl. Кроме этого, считается, что сила упругости вдоль всей пружины одинакова, так как масса пружины обычно не учитывается. Задача 1. При помощи пружинного динамометра поднимают с ускорением а = 2,5 м/с2, направленным вверх, груз массой m = 2 кг. Определите модуль удлинения пружины динамометра, если её жёсткость k = 1000 Н/м. Р е ш е н и е. Согласно закону Гука, выражающему связь между модулем внешней силы Для нахождения силы Направим ось OY вертикально вверх так, чтобы пружина была расположена вдоль этой оси (рис. 3.16). В проекции на ось OY второй закон Ньютона можно записать в виде mау = Fy + mgy.
Так как ау = a, gy = -g и Fy = F, то F = mа + mg = m(а + g). Следовательно,
Задача 2. Определите, как изменяется сила натяжения пружины, прикреплённой к бруску массой m = 5 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 30° до 60°. Трение не учитывайте. Р е ш е н и е. На брусок действуют сила тяжести, сила натяжения пружины и сила реакции опоры (рис. 3.17).
Условие равновесия бруска: m Запишем это условие в проекциях на оси ОХ и OY: Из первого уравнения системы получим Fyпp = mg sinα. При изменении угла наклона изменение силы упругости найдём из выражения ΔFyпp = mg(sinα2 - sinα1) = 5 • 10 • (0,866 - 0,5) (Н) = 18,3 Н.
|
|
|



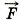 , вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда
, вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда 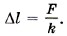
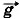 , действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m
, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m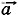 = F + m
= F + m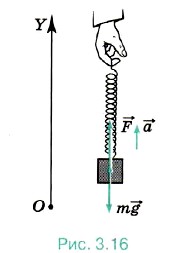
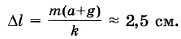
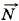 +
+