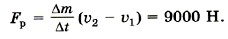|
|
|
|
|
Глава 4. Закон сохранения импульса Примеры решения задач по теме «Закон сохранения импульса»Р е ш е н и е. Так как скорости Согласно закону сохранения импульса имеем m1 Запишем это уравнение в проекциях на оси ОХ и OY, проведённые так, как показано на рисунке 4.3: m1υ1x + m2υ2x = (m1 + m2)их,
Так как υ1x = υ1, υ2x = 0, υ1y = 0, υ2y = υ2y = υ2, то
Модуль скорости и равен Итак, υ2 = и, следовательно, υ1 = 3и. Можно эту задачу решить так. Импульсы Тогда Задача 3. Компоненты топлива в двигатель ракеты подаются со скоростью υ1 = 200 м/с, а горючий газ выходит из сопла со скоростью υ2 = 500 м/с. Массовый расход топлива двигателем Р е ш е н и е. Изменение импульса топлива массой Δm за время Δt равно Δmυ2 - Δmυ1 = FΔt. Тогда сила, подействовавшая на горючий газ, вырывающийся из сопла ракеты,
Согласно третьему закону Ньютона сила, подействовавшая на топливо, равна по модулю и противоположна по направлению силе, подействовавшей на ракету, т. е. реактивной силе
Задачи для самостоятельного решения 1. Неподвижный вагон массой 2 • 104 кг сцепляется с платформой массой 3 • 104 кг. До сцепки платформа имела скорость 1 м/с. Чему равна скорость вагона и платформы после их сцепки? 2. На плот массой 100 кг, имеющий скорость 1 м/с, направленную вдоль берега, прыгает человек массой 50 кг со скоростью 1,5 м/с перпендикулярно берегу. Определите скорость плота с прыгнувшим на него человеком. 3. Будет ли увеличиваться скорость ракеты, если скорость истечения газов относительно ракеты меньше скорости самой ракеты и вытекающие из сопла газы летят вслед за ракетой? 4. Охотник стреляет с лёгкой надувной лодки. Определите скорость лодки после выстрела, если масса охотника 70 кг, масса дроби 35 г и средняя начальная скорость дробинок равна 320 м/с. Ствол ружья во время выстрела образует с горизонтом угол 60°.
|
|
|



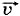 1 и
1 и 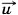 .
.
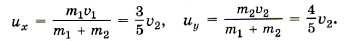
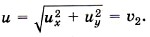
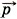 1 и
1 и 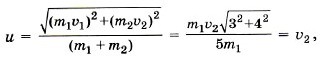 и, следовательно, υ1 = 3и.
и, следовательно, υ1 = 3и.
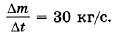 Определите реактивную силу.
Определите реактивную силу.
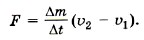
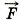 = -
= -