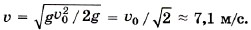|
|
|
|
|
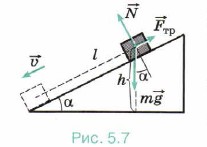
Глава 5. Закон сохранения энергии Примеры решения задач по теме «Кинетическая энергия и её изменение»Работа силы натяжения равна нулю, так как она всё время перпендикулярна перемещению. На основании закона о независимости движений движение шарика можно рассматривать как сумму двух движений: по оси ОХ и по оси OY. Работа силы тяжести при перемещении шарика вдоль оси ОХ равна нулю, так как сила тяжести перпендикулярна перемещению вдоль этой оси. Работа силы тяжести при перемещении вдоль оси OY равна Аm = mgΔy, где Δу = h1 - h2. Из треугольника АO2O1 получим O1O2 = lcosα0, тогда h1 = l - O1O2 = l(1 - cosα0), а из треугольника ВO2С получим O2С = lcosα, h2 = l - O2С = l(1 - cosα). Окончательно h1 - h2 = l(cosα - cosα0). Работа силы тяжести равна Аm = mgl(cosα - cosα0). Подставив найденное выражение для работы в уравнение (1), получим m22/2 = mgl(cosα - cosα0). Скорость в точке В: Перемещение шарика вдоль оси OY при движении из точки А в точку О равно h1. Тогда скорость шарика в точке О: Задача 3. Тело брошено вертикально вверх со скоростью υ0 = 10 м/с. Определите наибольшую высоту подъёма hmах, а также скорость тела на высоте, равной hmax/2. Силой сопротивления воздуха можно пренебречь. Р е ш е н и е. Изменение кинетической энергии тела при подъёме на максимальную высоту равно работе силы тяжести: 0 - mυ20/2 = -mghmax. Из этого уравнения сразу же получаем выражение для максимальной высоты подъёма: hmах = υ20/2g = 5 м. Скорость тела на некоторой высоте при падении равна его скорости на той же высоте при подъёме. Определим скорость тела при падении с максимальной высоты. Согласно теореме об изменении кинетической энергии mυ2/2 - 0 = mgh = mghmax/2. (Сила тяжести при спуске совершает положительную работу.) Тогда для скорости получаем формулу Задача 4. Груз тянут вверх по наклонной плоскости с углом а у основания. На высоте h верёвка обрывается. Определите скорость груза у основания плоскости. Коэффициент трения груза о плоскость равен μ. Р е ш е н и е. На груз действуют силы тяжести, нормальной реакции опоры и трения (рис. 5.7).
|
|
|



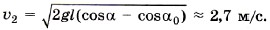
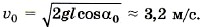
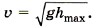 С учётом выражения для hmax окончательно получим
С учётом выражения для hmax окончательно получим