§ 12. «Математические начала натуральной философии» Ньютона

Применение научного метода Ньютоном

1. Английский физик Ньютон, как и некоторые другие учёные — его предшественники и современники, — предпринял попытку дать объяснение многочисленных разрозненных фактов, полученных в ходе опытов и наблюдений. Основным законом, с помощью которого можно было объяснить эти факты, Ньютон считал закон всемирного тяготения. Как вы уже знаете, обоснование этого закона, его формулировка и математическая запись стали основными целями создания труда «Математические начала натуральной философии».

Английский физик Ньютон

Исаак Ньютон (1643—1727) — выдающийся английский учёный, создатель классической физики, член Лондонского королевского общества и Парижской академии наук.

Известен своими работами в области механики, математики, оптики, астрономии. Сформулировал основные законы и понятия классической механики; открыл закон всемирного тяготения; разработал теорию движения небесных тел; при помощи трёхгранной стеклянной призмы разложил белый свет в спектр; объяснил происхождение цветов; сконструировал телескоп-рефлектор.

После изучения и анализа опытных фактов и результатов наблюдений Ньютон, следуя своему методу, вывел общие постулаты, которые сегодня в память о великом учёном называют законами динамики Ньютона.

Первый закон Ньютона

2. В качестве первого постулата Ньютон назвал принцип инерции, сформулированный Галилеем, несколько уточнив его. В частности, Галилей, в отличие от Ньютона, относил к движению по инерции случай движения по окружности с постоянной по модулю скоростью. Поправки в формулировку закона вносились и после Ньютона. Наиболее важной из них является поправка о том, что принцип инерции выполняется только в инерциальных системах отсчёта. С учётом этого первый закон Ньютона формулируется так:

существуют системы отсчёта, относительно которых тело в отсутствие внешнего воздействия сохраняет своё состояние равномерного прямолинейного движения или покоя.

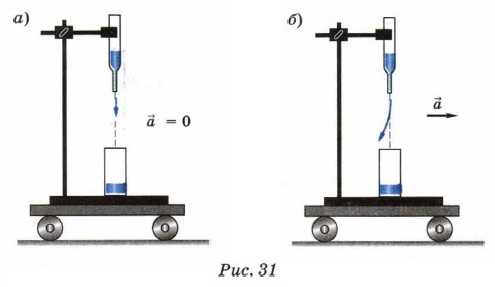
Такие системы отсчёта называют инерциальными. Первый закон Ньютона ещё называют законом инерции.

В быту возникают ситуации, когда тело в отсутствие внешнего воздействия начинает двигаться ускоренно. Традиционный пример подобного явления — падение вперёд стоящего в автобусе пассажира при резком торможении. Пассажир, покоившийся до начала торможения относительно системы отсчёта, связанной с автобусом, в момент торможения начинает ускоренно двигаться. При этом нельзя указать тело, под действием которого пассажир меняет скорость относительно автобуса. Однако ничего парадоксального в этом явлении нет: просто в данном случае рассматривается движение пассажира относительно автобуса, который при торможении движется ускоренно относительно земли. Система отсчёта, связанная с автобусом, является неинерциальной. Если рассмотреть то же явление относительно системы отсчёта, связанной с землёй, можно наблюдать действие первого закона Ньютона: при торможении пассажир падает, так как, согласно закону инерции, продолжает двигаться относительно земли, поскольку нет силы, заставляющей его остановиться. Систему отсчёта, связанную с землёй, в данном случае можно считать инерциальной.

Проделаем опыт. Укрепим на штативе капельницу и поставим на основание штатива мензурку таким образом, чтобы вода из капельницы падала прямо в неё. Будем перемещать штатив, установив его на тележке, по горизонтальной поверхности стола. В случае равномерного движения тележки (рис. 31, а) капли будут попадать в мензурку так же, как если бы тележка покоилась. При ускоренном движении тележки (рис. 31, б) капли из капельницы в мензурку не попадут. Таким образом, в первом случае систему отсчёта, связанную с тележкой, можно считать инерциальной, а во втором — нет.

равномерного движения тележки

Заметим, что, строго говоря, нет ни одной системы отсчёта, связанной с реальным телом, которую можно было бы считать инерциальной. Инерциальная система отсчёта — это идеализированное понятие.

Однако во многих реальных ситуациях можно с достаточной точностью считать инерциальной систему отсчёта, связанную с землёй, поскольку ускоренное движение Земли не оказывает существенного влияния на многие механические явления, происходящие вблизи её поверхности. При необходимости более точных расчётов в качестве инерциальных рассматриваются системы отсчёта, связанные с удалёнными от Земли небесными телами — Солнцем и звёздами.

Продолжение >>>