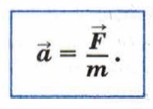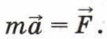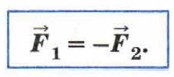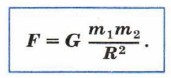Главная >> Физика. 10 класс. Базовый уровень. Пурышева

Глава 2. Ядро классической механики

«Математические начала натуральной философии» Ньютона

Второй закон Ньютона

3. Вы уже знаете, что в ходе опытов с шаром и наклонной плоскостью Галилей установил, что под действием постоянной силы тело движется равноускоренно. Если Галилей обобщил этот вывод для случая свободного падения, то Ньютон, проанализировав ещё и другие опытные факты, сделал более широкое обобщение и постулировал, что

ускорение, приобретаемое телом, прямо пропорционально действующей на него силе и обратно пропорционально массе тела.

Этот постулат называют вторым законом Ньютона и математически записывают так:

Второй закон Ньютона иногда записывают и в таком виде:

Третий закон Ньютона

4. Свой третий постулат Ньютон сформулировал так:

действию всегда есть равное и противоположное противодействие: взаимные действия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Говоря о равенстве сил по третьему закону Ньютона, необходимо уточнить, что силы:

— действуют вдоль одной прямой;

— имеют одинаковую природу.

Математическая запись третьего закона Ньютона такова:

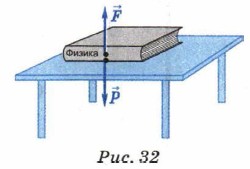
Действие закона можно наблюдать даже в самых простых ситуациях, например когда книга лежит на столе: книга давит на поверхность стола своим весом вертикально вниз, а стол действует на книгу силой упругости в противоположном направлении (рис. 32). Действие закона можно наблюдать и в более сложных ситуациях.

Закон всемирного тяготения

5. Согласно закону всемирного тяготения,

все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Этот закон впервые обосновал, сформулировал и записал математически Ньютон. Открытие закона всемирного тяготения позволило объяснить множество эмпирических фактов, накопленных в ходе астрономических наблюдений. Однако именно Ньютон сумел понять и доказать, что многие механические явления, происходящие в космическом пространстве и на Земле, объясняются действием одних и тех же сил — сил тяготения, называемых гравитационными силами. Именно гравитационные силы заставляют Луну обращаться вокруг Земли, а Землю — вокруг Солнца. И эти же силы приводят к падению на поверхность Земли снаряда, выпущенного из пушки, или мяча, подброшенного вверх.

Значение коэффициента G, называемого гравитационной постоянной, впервые было экспериментально определено в 1798 г. английским физиком Генри Кавендишем (1731 —1810). В дальнейшем значение G было определено более точно, и сегодня гравитационную постоянную считают равной

G = 6,67259 • 10¹¹ Н • м²/кг².

Ускорение свободного падения

6. Вам хорошо известна формула, которая позволяет вычислить силу тяжести:

F_тяж = mg.

Её можно получить из закона всемирного тяготения.

Рассмотрим случай взаимодействия Земли и тела массой m₁, находящегося на её поверхности (рис. 33), обозначив массу и радиус Земли соответственно М₃ и R₃. В рассматриваемой ситуации расстояние между телами будет равно радиусу Земли, и поэтому:

<<< К началу      Окончание >>>