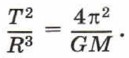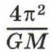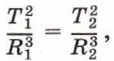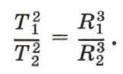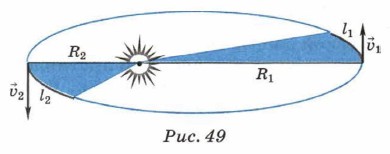
|
|
|
|
|
Глава 3. Следствия классической механики
Небесная механикаЗаконы Кеплера3. Рассмотренные примеры движения спутника иллюстрируют, как классическая механика даёт объяснение первого закона Кеплера. Планеты Солнечной системы, являясь своеобразными спутниками Солнца, движутся вокруг него по эллиптическим орбитам. Поскольку форма орбиты определяется скоростью движения планеты, то очевидно, что скорость каждой планеты меньше, чем значение параболической скорости, соответствующей массе Солнца и расстоянию от него до данной планеты. В противном случае планеты не удерживались бы Солнцем на орбитах. В то же время скорость каждой планеты больше, чем значение соответствующей круговой скорости. Теория Ньютона позволяет не только дать объяснение первого закона Кеплера, но и обобщить его. Любое тело под действием силы тяготения движется по одной из трёх кривых — эллипсу, параболе или гиперболе. При движении тела по эллипсу в одном из его фокусов находится другое тело, со стороны которого и действует сила тяготения. Первый закон Кеплера, сформулированный таким образом, позволяет описывать не только движение планет, но и других тел, движущихся под действием сил тяготения. Опуская математические расчёты, проиллюстрируем объяснение второго закона Кеплера. Если бы планеты двигались по круговым траекториям, то их линейные скорости определялись бы формулой (3). Поскольку орбита планеты — эллипс и Солнце находится в одном из его фокусов, то расстояние от Солнца до планеты постоянно изменяется. Но, как вам известно, любое криволинейное движение, в том числе и движение по эллипсу, можно с достаточной точностью представить как движение по окружностям разных радиусов. Таким образом, чем дальше планета от Солнца на своей орбите, тем меньше её линейная скорость (рис. 49). А это значит, что планета, находясь ближе к Солнцу, за некоторый промежуток времени проходит больший путь, чем путь, пройденный за такой же промежуток времени, когда планета находится дальше от Солнца. Это и определяет равенство площадей, описываемых радиусом планеты за равные промежутки времени.
Третий закон Кеплера можно вывести, считая, что планеты движутся по круговым орбитам (это приближение не очень грубое, поскольку орбиты планет Солнечной системы мало отличаются от окружностей). Запишем линейную скорость планеты как отношение длины окружности её орбиты к периоду обращения:
Поскольку планета движется по окружности, то полученное отношение равно значению круговой скорости:
где М — масса Солнца. Из этого равенства получаем:
или
Значение дроби
или
|
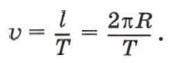
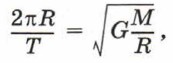
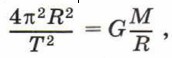есть величина постоянная, следовательно, отношение периода обращения в квадрате к расстоянию от Солнца в кубе одинаково для любой планеты, т. е.
|
|